일반화 회귀에서 모형 비교 테이블의 예
이 예에서는 6개의 예측 변수가 있는 개수 반응에 대한 여러 예측 모형을 개발합니다. 개수 반응은 Poisson 분포를 사용하여 모델링됩니다. 네 가지 예측 모형은 Lasso 회귀, Elastic Net, 적응형 Lasso 회귀 및 적응형 Elastic Net입니다. 일반화 회귀의 모형 비교 보고서를 사용하여 네 가지 예측 모형을 서로 비교하고 최대 가능도 모형과도 비교하여 최종 모형을 선택합니다.
1. 도움말 > 샘플 데이터 폴더를 선택하고 Liver Cancer.jmp를 엽니다.
2. 분석 > 모형 적합을 선택합니다.
3. "열 선택" 목록에서 Node Count를 선택하고 Y를 클릭합니다.
4. BMI ~ Jaundice를 선택하고 매크로 > 특정 차수까지의 요인을 클릭합니다.
이렇게 하면 차수 2(차수 상자의 기본값)까지의 모든 항이 모형에 추가됩니다.
5. "열 선택" 목록에서 Validation을 선택하고 검증을 클릭합니다.
6. "분석법" 목록에서 일반화 회귀를 선택합니다.
7. "분포" 목록에서 Poisson을 선택합니다.
8. 실행을 클릭합니다.
"모형 비교" 보고서, "모형 시작" 제어판 및 "검증 열을 사용한 Poisson 최대 가능도" 보고서가 포함된 "일반화 회귀" 보고서가 나타납니다. 기본 추정 방법은 "Lasso 회귀"입니다.
Lasso 회귀 모형 적합
9. 시작을 클릭합니다.
Elastic Net 모형 적합
10. 보고서 창 상단으로 스크롤하여 "모형 시작" 개요를 엽니다.
11. "추정 방법"에서 Elastic Net을 선택합니다.
12. 시작을 클릭합니다.
적응형 Lasso 회귀 모형 적합
13. 보고서 창 상단으로 스크롤하여 "모형 시작" 개요를 엽니다.
14. "추정 방법"에서 Lasso 회귀를 선택합니다.
15. 적응형 상자를 선택합니다.
16. 시작을 클릭합니다.
적응형 Elastic Net 모형 적합
17. 보고서 창 상단으로 스크롤하여 "모형 시작" 개요를 엽니다.
18. "추정 방법"에서 Elastic Net을 선택합니다.
참고: 이전 모형에서 "적응형" 상자가 선택되어 있는지 확인합니다.
19. 시작을 클릭합니다.
모형 비교
20. 보고서 창 맨 위로 스크롤합니다.
21. "모형 비교" 테이블에서 "검증 일반화 R²" 열 머리글을 클릭합니다.
그림 7.8 모형 비교 보고서
이제 "모형 비교" 테이블이 검증 일반화 R² 값에 따라 오름차순으로 정렬됩니다. 이러한 R² 값은 모형이 검증 데이터 집합에 얼마나 잘 적합되는지를 나타냅니다. 최대 가능도 모형의 검증 일반화 R² 값은 음수이며 이는 과대적합을 나타냅니다. 벌점 방법은 모두 최대 가능도 모형보다 검증 데이터를 더 잘 적합시킵니다. 벌점 모형 중 검증 데이터에 특별히 잘 적합되는 모형은 없지만 적응형 방법이 비적응형 방법보다 더 잘 적합됩니다. 적응형 Elastic Net 방법이 검증 데이터에 대해 가장 잘 작동하므로 예측에 사용하기로 결정합니다.
22. "적응형 Elastic Net" 행을 제외하고 "표시" 아래의 모든 상자를 선택 해제합니다.
23. "검증 열을 사용한 Poisson 적응형 Elastic Net" 옆의 빨간색 삼각형을 클릭하고 0이 아닌 항 선택을 선택합니다.
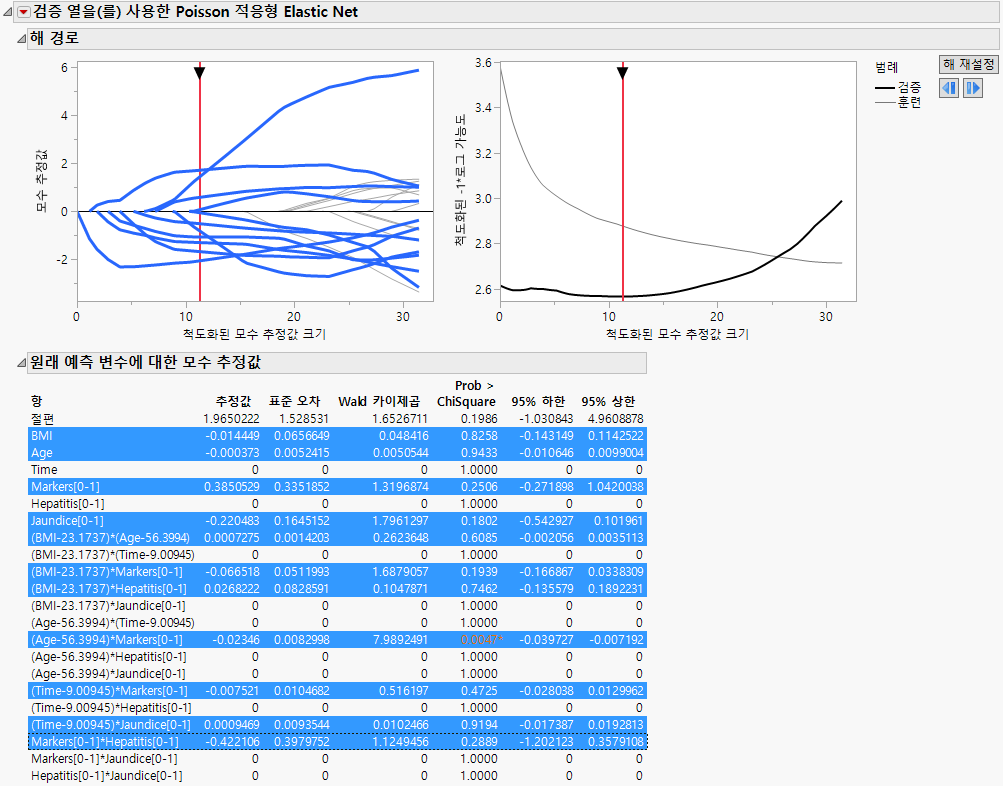
그림 7.9 0이 아닌 항이 강조 표시된 적응형 Elastic Net 적합의 해 경로
적응형 Elastic Net 모형에서 0이 아닌 항이 "해 경로" 및 "모수 추정값" 테이블에서 선택됩니다.
이제 이 모형을 예측에 사용하거나, 예측 프로파일러를 열어 모수가 반응 변수에 미치는 영향을 더 자세히 탐색할 수 있습니다.