ALT 설계의 고장 분포
가속 수명 시험 설계 플랫폼에서는 로그 정규 또는 Weibull 고장 분포를 선택할 수 있습니다. 이 섹션에는 각 분포의 pdf(확률 밀도 함수)와 cdf(누적 분포 함수)에 대한 파라미터화가 포함되어 있습니다. Weibull 분포에 대한 자세한 내용은 신뢰성 및 생존 방법의 수명 분포에서 확인하십시오.
로그 정규
로그 정규 분포는 데이터 범위가 10의 여러 거듭제곱일 경우 고장 시간을 나타내는 데 흔히 사용됩니다. 보통 이 분포는 독립적이며 같은 분포를 따르는 다수의 작은 양수 확률 변수의 곱으로 개념화됩니다. 이 분포는 데이터 값의 로그가 정규 분포로 나타날 때 적절합니다. 일반적으로 확률 분포 함수는 강한 오른쪽 왜도가 특징입니다.
로그 정규 계열은 위치 모수(m)와 형상 모수(s)로 파라미터화됩니다. 로그 정규 pdf 및 cdf는 다음과 같이 지정되며, 여기서 로그는 밑이 e입니다.
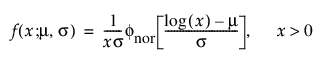
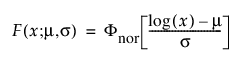 ,
,
아래 함수는
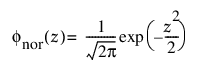
및
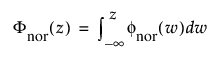
각각 표준 정규 분포(N(0,1))에 대한 pdf와 cdf입니다.
Weibull
Weibull 분포를 사용하면 위험률이 증가하거나 감소하는 고장 시간 데이터를 모델링할 수 있습니다. 이 분포는 형상 모수 값을 기반으로 다양한 유형의 데이터를 모델링할 때 엄청난 유연성을 제공하므로 신뢰성 분석에 자주 사용됩니다.
일반적으로 Weibull pdf와 cdf는 다음과 같이 나타냅니다.
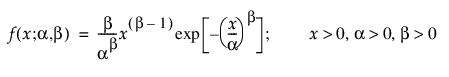
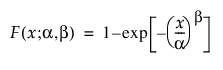
여기서 a는 척도 모수이고 b는 형상 모수입니다. Weibull 분포는 b = 1일 때 지수 분포로 축소됩니다.
Weibull 파라미터화
JMP에서 Weibull 파라미터화는 s를 척도 모수로, m를 위치 모수로 정의합니다. 이 모수는 다음과 같이 a 및 b Weibull 파라미터화와 관련됩니다.
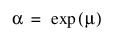
및
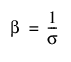
이러한 모수를 사용할 경우 Weibull 분포의 pdf와 cdf는 m = log(a) 및 s = 1/b인 위치-척도 파라미터화를 사용하여 로그 변환된 SEV(최소 극단값 분포)로 표현됩니다.
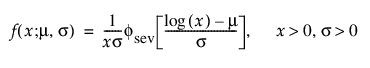
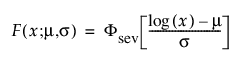
여기서,
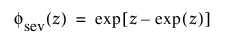
및
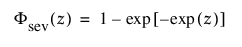
각각 표준화된 최소 극단값(m = 0, s = 1) 분포에 대한 pdf와 cdf입니다.