비례 위험 모형 적합 플랫폼 개요

비례 위험 모형은 설명 변수가 생존 시간에 미치는 영향을 조사하기 위해 D. R. Cox(1972)가 제안한 특수 준모수 회귀 모형입니다. 모집단의 각 멤버에 대한 생존 시간은 자체의 위험 함수를 따르는 것으로 가정합니다.

비례 위험 모형은 지정되지 않은 임의의 기준 위험 함수를 포함한다는 점에서 비모수 모형입니다. 공변량에 대한 모수 형식을 가정하므로 모수 모형입니다. 기준 위험 함수는 일반적인 위험 함수를 제공하기 위해 모형의 공변량(시간에 따라 변하지 않음) 함수로 척도화됩니다. Kaplan-Meier 분석과 달리 비례 위험은 모수 추정값 및 각 공변량의 표준 오차를 계산합니다. 설명 변수와 관련된 회귀 모수(b) 및 표준 오차는 최대 가능도 방법을 사용하여 추정됩니다. 또한 조건부 위험 비율도 모수 추정값에서 계산됩니다.

비례 위험의 생존 추정값은 경험적 방법을 사용하여 생성됩니다. 자세한 내용은 Lawless(1982)에서 확인하십시오. 이러한 값은 생존 함수 S(t)의 경험적 누적 위험 함수 추정값 H(t)를 나타내며, S0 = exp(-H(t))로 쓸 수 있습니다. 위험 함수는 다음과 같이 정의됩니다.

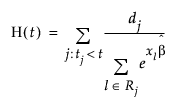
반응에 동점이 있는 경우, 즉 주어진 시간 사건에 두 개 이상의 고장이 있는 경우 Breslow 가능도가 사용됩니다.