정규 분포의 공정 능력 지수에 대한 통계 상세 정보
이 섹션에서는 공정 능력 플랫폼에서 정규 데이터에 대한 공정 능력 지수 계산에 대해 자세히 설명합니다.
평균이 m이고 표준편차가 s인 공정 특성에 대한 모집단 기반 공정 능력 지수는 다음과 같이 정의됩니다. 표본 관측값의 경우 모수가 다음 추정값으로 대체됩니다.
Cp =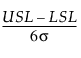 
Cpl =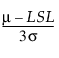 
Cpu =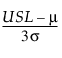 
Cpk =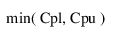 
Cpm =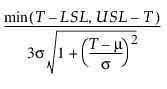 
목표 지수 =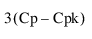 
이 계산식에서는 다음과 같은 표기를 사용합니다.
LSL = 규격 하한
USL = 규격 상한
T = 목표값
군내 표준편차 공정 능력 추정값의 경우 사용자가 선택한 부분군 지정 방법을 사용하여 s를 추정합니다. 전체 표준편차 공정 능력 추정값의 경우 표본 표준편차를 사용하여 s를 추정합니다. 규격 한계가 하나뿐인 경우 결측 규격 한계를 포함하는 공정 능력 지수가 결측값으로 보고됩니다.
참고: 기본 AIAG(Ppk) 라벨을 사용하면 전체 표준편차를 기반으로 하는 지수가 Pp, Ppl, Ppu 및 Ppk로 표시됩니다. 전체 표준편차를 사용할 때 Cpm 지수의 라벨은 변경되지 않습니다. 이 섹션의 계산식은 Cp 라벨을 사용하여 정의됩니다.
공정 능력 지수에 대한 신뢰 구간
공정 능력 지수에 대한 신뢰 구간은 정규 분포를 따르는 공정에만 사용할 수 있습니다. 신뢰 구간은 군내 표준편차 및 전체 표준편차 공정 능력에 대해 모두 계산되며 "개별 상세 정보 보고서"에 표시됩니다.
Cp
Cp에 대한 100(1 - a)% 신뢰 구간은 다음과 같이 계산됩니다.
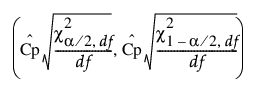
다음은 각 요소에 대한 설명입니다.
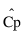= Cp에 대한 추정값
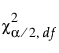= 자유도가 df인 카이제곱 분포의 (a/2)번째 분위수
df = 자유도
N = 관측값 수
m = 부분군 수
전체 표준편차 공정 능력의 경우 자유도는 N - 1입니다.
군내 표준편차 공정 능력의 경우 자유도는 부분군 지정 및 군내 표준편차 추정 방법에 따라 달라집니다.
• 불균형 부분군을 사용하는 군내 표준편차 공정 능력의 경우 자유도 계산은 군내 표준편차 추정 방법에 관계없이 동일합니다. 자유도는 N - m입니다.
• 균형 부분군(크기 n = N/m)을 사용하는 군내 표준편차 공정 능력의 경우 자유도 계산은 군내 표준편차 추정 방법에 따라 달라집니다.
– 비편향 표준편차의 평균을 사용하여 군내 표준편차를 추정하는 경우 자유도는 f * (N - m)입니다. 배율 f는 0.875와 1 사이에서 변하며 다음과 같이 정의됩니다.
여기서 G(n)는 n에서 실행된 감마 함수입니다.
자세한 내용은 Bissell 연구 자료(1990)에서 확인하십시오.
– 범위 평균을 사용하여 군내 표준편차를 추정하는 경우 자유도는 df = 1/A - (3/16) * A + (3/64) * A2 + 0.25로 계산됩니다. A는 다음과 같이 정의됩니다.
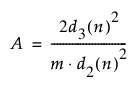
d2(n) = 단위 표준편차를 갖는 n개 독립 정규 분포 변수의 범위 기대값
d3(n) = 단위 표준편차를 갖는 n개 독립 정규 분포 변수의 범위 표준편차
자세한 내용은 David 연구 자료(1951)에서 확인하십시오.
– 비편향 합동 표준편차를 사용하여 군내 표준편차를 추정하는 경우 자유도는 N - m입니다.
• 부분군이 없는 군내 표준편차 공정 능력의 경우 자유도 계산은 군내 표준편차 추정 방법에 따라 달라집니다.
– 평균 이동 범위를 사용하여 군내 표준편차를 추정하는 경우 자유도는 0.62 * (N - 1)로 계산됩니다.
– 이동 범위 중앙값을 사용하여 군내 표준편차를 추정하는 경우 자유도는 0.32 * (N - 1)로 계산됩니다.
자세한 내용은 Wheeler 연구 자료(2004, p. 82)에서 확인하십시오.
Cpk
Cpk에 대한 100(1 - a)% 신뢰 구간은 다음과 같이 계산됩니다.
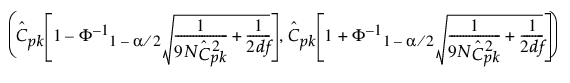
다음은 각 요소에 대한 설명입니다.
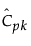= Cpk에 대한 추정값
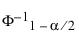= 표준 정규 분포의 (1 - a/2)번째 분위수
df = 자유도
N = 관측값 수
m = 부분군 수
전체 표준편차 공정 능력의 경우 자유도는 N - 1입니다.
군내 표준편차 공정 능력의 경우 자유도는 부분군 지정 및 군내 표준편차 추정 방법에 따라 달라집니다.
• 불균형 부분군을 사용하는 군내 표준편차 공정 능력의 경우 자유도 계산은 군내 표준편차 추정 방법에 관계없이 동일합니다. 자유도는 N - m입니다.
• 균형 부분군(크기 n = N/m)을 사용하는 군내 표준편차 공정 능력의 경우 자유도 계산은 군내 표준편차 추정 방법에 따라 달라집니다.
– 비편향 표준편차의 평균을 사용하여 군내 표준편차를 추정하는 경우 자유도는 f * (N - m)입니다. 배율 f는 0.875와 1 사이에서 변하며 다음과 같이 정의됩니다.
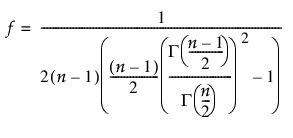
여기서 G(n)는 n에서 실행된 감마 함수입니다.
자세한 내용은 Bissell 연구 자료(1990)에서 확인하십시오.
– 범위 평균을 사용하여 군내 표준편차를 추정하는 경우 자유도는 df = 1/A - (3/16) * A + (3/64) * A2 + 0.25로 계산됩니다. A는 다음과 같이 정의됩니다.
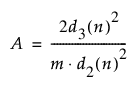
d2(n) = 단위 표준편차를 갖는 n개 독립 정규 분포 변수의 범위 기대값
d3(n) = 단위 표준편차를 갖는 n개 독립 정규 분포 변수의 범위 표준편차
자세한 내용은 David 연구 자료(1951)에서 확인하십시오.
– 비편향 합동 표준편차를 사용하여 군내 표준편차를 추정하는 경우 자유도는 N - m입니다.
• 부분군이 없는 군내 표준편차 공정 능력의 경우 자유도 계산은 군내 표준편차 추정 방법에 따라 달라집니다.
– 평균 이동 범위를 사용하여 군내 표준편차를 추정하는 경우 자유도는 0.62 * (N - 1)로 계산됩니다.
– 이동 범위 중앙값을 사용하여 군내 표준편차를 추정하는 경우 자유도는 0.32 * (N - 1)로 계산됩니다.
자세한 내용은 Wheeler 연구 자료(2004, p. 82)에서 확인하십시오.
Cpm
참고: Cpm에 대한 신뢰 구간은 목표값이 규격 하한과 규격 상한 사이에서 중심화되는 경우에만 계산됩니다.
Cpm에 대한 100(1 - a)% 신뢰 구간은 다음과 같이 계산됩니다.
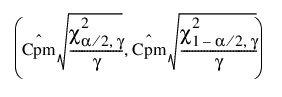
다음은 각 요소에 대한 설명입니다.
= Cpm에 대한 추정값
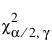= 자유도가 g인 카이제곱 분포의 (a/2)번째 분위수
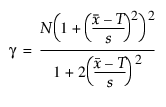
N = 관측값 수
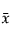= 관측값의 평균
T = 목표값
s = 표준편차 추정값
전체 표준편차 공정 능력의 경우 s는 전체 표준편차 추정값입니다. 군내 표준편차 공정 능력의 경우 s는 군내 표준편차 추정값으로 대체됩니다.
팁: Cp, Cpk, Cpm의 신뢰 구간에 대한 자세한 내용은 Pearn & Kotz(2006)에서 확인하십시오.
Cpl, Cpu
Cpl과 Cpu의 신뢰 하한 및 상한은 Chou et al. (1990)의 방법을 사용하여 계산됩니다.
Cpl에 대한 100(1 - a)% 신뢰 한계(CPLL, CPLU로 표시)는 다음 방정식을 충족합니다.
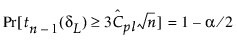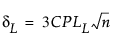
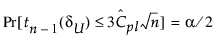여기서, 
여기서,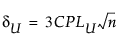 
다음은 각 요소에 대한 설명입니다.
tn-1(d)은 n - 1 자유도와 비중심성 모수 d를 사용하는 비중심 t 분포를 따릅니다.
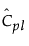= Cpl에 대한 추정값
Cpu에 대한 100(1 - a)% 신뢰 한계(CPUL, CPUU로 표시)는 다음 방정식을 충족합니다.
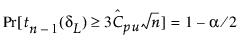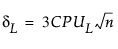
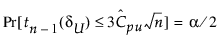여기서, 
여기서,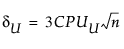 
다음은 각 요소에 대한 설명입니다.
tn-1(d)은 n - 1 자유도와 비중심성 모수 d를 사용하는 비중심 t 분포를 따릅니다.
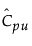= Cpu에 대한 추정값