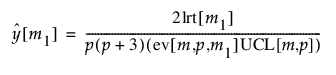변화 지점 감지에 대한 통계 상세 정보
이 섹션에는 다변량 관리도 플랫폼의 "변화 지점 감지" 옵션에 대한 상세 정보가 포함되어 있습니다. 이 섹션의 설명은 Sullivan and Woodall(2000)에서 발전된 내용을 기반으로 합니다.
가정
평균 벡터가 mi이고 공분산 행렬이 Si인 p 차원의 다변량 분포를 Np(mi,Si)로 나타냅니다. 다음과 같이 xi를 이러한 분포와 독립적인 m(m > p)개의 관측값이라고 가정해 보겠습니다.
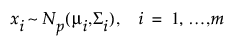
공정이 안정적이면 평균 mi 및 공분산 행렬 Si가 공통 값과 동일하여 xi가 Np(m, S) 분포를 따릅니다.
m1개 관측값과 m1+1개 관측값 사이에 평균 벡터와 공분산 행렬 중 하나 또는 둘 다에서 단일 변화가 발생한다고 가정해 보겠습니다. 그러면 다음 조건이 충족됩니다.
• 1 ~ m1 관측값은 평균 벡터 및 공분산 행렬이 동일합니다(ma,Sa).
• m1 + 1 ~ m 관측값은 평균 벡터 및 공분산 행렬이 동일합니다(mb,Sb).
• 다음 중 하나가 발생합니다.
– 변화가 평균에 영향을 미치는 경우 ma ¹ mb입니다.
– 변화가 공분산 행렬에 영향을 미치는 경우 Sa ¹ Sb입니다.
– 변화가 평균과 공분산 행렬에 모두 영향을 미치는 경우 ma ¹ mb, Sa ¹ Sb입니다.
개요
가능도비 검정 방법은 평균 벡터와 공분산 행렬 중 하나 또는 둘 다에서 발생하는 변화를 식별하는 데 사용됩니다. 가능도비 검정 통계량은 근사 관리 상한이 1인 관리도 통계량을 계산하는 데 사용됩니다. 가능한 모든 m1 값에 대해 관리도 통계량이 표시됩니다. 관측값의 관리도 통계량이 관리 상한 1을 초과하면 변화가 발생했음을 나타냅니다. 변화가 정확히 한 번 발생한다고 가정하면 관리도 통계량 값이 최대인 관측값 직후에 변화가 시작된다고 간주됩니다.
가능도비 검정 통계량
처음 m1개 관측값에 대한 로그 가능도 함수의 두 배인 최대값은 다음과 같이 정의됩니다.
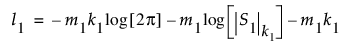
l1에 대한 방정식에서는 다음과 같은 표기를 사용합니다.
• S1은 처음 m1개 관측값에 대한 공분산 행렬의 최대 가능도 추정값입니다.
• k1 = Min[p,m1-1]은 p x p 행렬 S1의 계수입니다.
• 
표기는 S1 행렬의 일반화된 행렬식을 나타내며, 다음과 같이 k1개의 양의 고유값 lj에 대한 곱으로 정의됩니다.
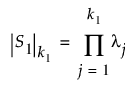
일반화된 행렬식은 S1이 완전 계수를 가질 때 보통 행렬식과 같습니다.
후속 m2 = m - m1개 관측값에 대한 로그 가능도 함수의 두 배인 최대값을 l2로 나타내고, 모든 m개 관측값에 대한 로그 가능도 함수의 두 배인 최대값을 l0으로 나타냅니다. l2와 l0 모두 l1에 제공된 것과 비슷한 표현식이 제공됩니다.
가능도비 검정 통계량은 l1 + l2 합을 l0과 비교합니다. l1 + l2 합은 m1에서 변화가 발생할 수 있다고 가정하는 로그 가능도의 두 배입니다. l0 값은 변화가 없다고 가정하는 로그 가능도의 두 배입니다. l0이 l1 + l2보다 많이 작으면 공정이 불안정하다고 가정합니다.
관측값 m1 + 1에서 변화가 시작되는지 여부를 검정하는 경우 가능도비 검정 통계량은 다음과 같이 정의됩니다.
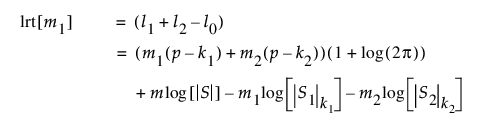
가능도비 검정 통계량은 자유도가 p(p + 3)/2인 점근적 카이제곱 분포를 따릅니다. 로그 가능도비 값이 크면 공정이 불안정하다는 것을 나타냅니다.
관리도 통계량
시뮬레이션에 따르면 lrt[m1]의 기대값은 계열에서 관측값의 위치를 기반으로 하며, 특히 p와 m에 따라 달라집니다. 자세한 내용은 Sullivan and Woodall 연구 자료(2000)에서 확인하십시오.
lrt[m1]의 기대값을 구하는 근사 계산식은 시뮬레이션을 통해 도출됩니다. p에 대한 기대값의 종속성을 줄이기 위해 lrt[m1]을 점근적 기대값 p(p + 3)/2로 나눕니다.
p(p+3)/2로 나눈 lrt[m1]의 근사 기대값을 구하는 계산식은 다음과 같이 정의됩니다.
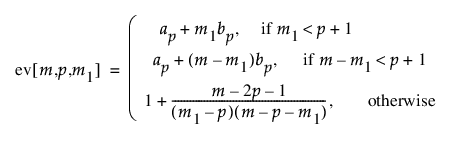
여기서,
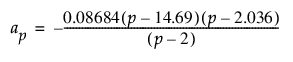
및
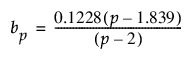
p = 2의 경우 m1 또는 m2 = 2일 때 ev[m,p,m1] 값은 1.3505입니다.
참고: p > 12 또는 m < (2p + 4)일 때는 위의 계산식이 정확하지 않습니다. 이러한 경우 시뮬레이션을 사용하여 근사 기대값을 구해야 합니다.
공정이 안정적이라고 가정할 때 약 0.05의 확률로 잘못된 관리이탈 신호를 생성하는 근사 관리 상한은 다음과 같이 계산됩니다.
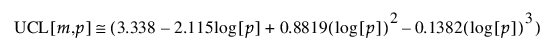
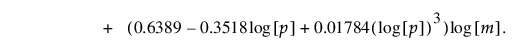
이 계산식은 m과 p에 따라 달라집니다.
관리도 통계량은 가능도비 검정 통계량 로그의 두 배를 p(p + 3), 근사 기대값 및 관리 한계 근사값으로 나눈 값으로 정의됩니다. UCL의 근사값으로 나누었으므로 관리 상한 1에 대해 관리도 통계량을 표시할 수 있습니다. 근사 관리도 통계량은 다음과 같이 계산됩니다.
