지수 평활 모형에 대한 통계 상세 정보
평활 모형은 다음과 같이 정의됩니다.
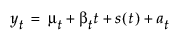
다음은 각 요소에 대한 설명입니다.
mt = 시간에 따라 변하는 평균 항
bt = 시간에 따라 변하는 기울기 항
s(t) = 시간에 따라 변하는 계절 항 중 하나
at = 확률 충격
추세가 없는 모형은 bt = 0이고 비계절 모형은 s(t) = 0입니다. 시간에 따라 변하는 이러한 항의 추정량은 다음과 같이 정의됩니다.
Lt = mt를 추정하는 평활 수준
Tt = bt를 추정하는 평활 추세
St - j(j = 0, 1,..., s - 1) = s(t)의 추정값
각 평활 모형은 이러한 추정량의 진화를 설명하는 재귀 평활 방정식 집합을 정의합니다. 평활 방정식은 평활 가중치라고 하는 다음 모형 모수로 작성됩니다.
a = 수준 평활 가중치
g = 추세 평활 가중치
j = 진폭감소 추세 가중치
d = 계절 평활 가중치
이러한 모수는 각 모형에 서로 다른 방식으로 입력(또는 전혀 입력되지 않음)되지만 가중치가 클수록 최근 데이터에 영향을 많이 주고 가중치가 작을수록 최근 데이터에 영향을 적게 준다는 공통된 특성이 있습니다. 평활 가중치에 대한 자세한 내용은 SAS/ETS 15.2 User’s Guide의 "Forecasting Process Details" 장에서 확인하십시오.
단순 지수 평활
단순 지수 평활 모형은 yt = mt + at입니다.
평활 방정식 Lt = ayt + (1 – a)Lt-1은 단일 평활 가중치 a로 정의됩니다. 이 모형은 다음 조건이 참일 때 ARIMA(0, 1, 1) 모형과 동일합니다.
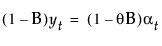 여기서,
여기서, 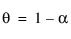
모형의 이동 평균 형식은 다음과 같이 정의됩니다.
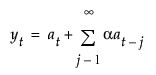
이중 (Brown) 지수 평활
이중 지수 평활 모형은 yt = mt + b1t + at입니다.
평활 방정식은 단일 평활 가중치 a를 사용하여 다음과 같이 정의됩니다.
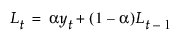
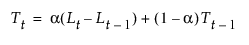
이 모형은 다음 조건이 참일 때 ARIMA(0, 1, 1)(0, 1, 1)1 모형과 동일합니다.
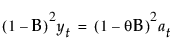 여기서
여기서 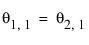 ,
, 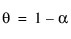
모형의 이동 평균 형식은 다음과 같이 정의됩니다.
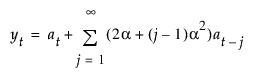
선형 (Holt) 지수 평활
선형 지수 평활 모형은 yt = mt + btt + at입니다.
평활 방정식은 a 및 g 평활 가중치를 사용하여 다음과 같이 정의됩니다.
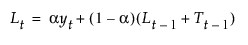
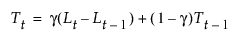
이 모형은 다음 조건이 참일 때 ARIMA(0, 2, 2) 모형과 동일합니다.
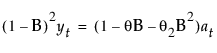 여기서
여기서 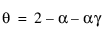 ,
, 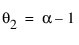
모형의 이동 평균 형식은 다음과 같이 정의됩니다.
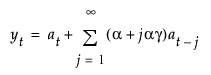
진폭감소 추세 선형 지수 평활
진폭감소 추세 선형 지수 평활 모형은 yt = mt + btt + at입니다.
평활 방정식은 a, g 및 j 평활 가중치를 사용하여 다음과 같이 정의됩니다.
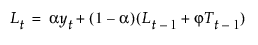
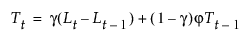
이 모형은 다음 조건이 참일 때 ARIMA(1, 1, 2) 모형과 동일합니다.
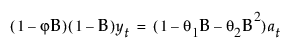
다음은 각 요소에 대한 설명입니다.
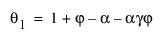
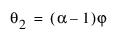
모형의 이동 평균 형식은 다음과 같이 정의됩니다.
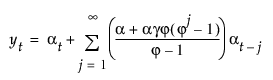
계절 지수 평활
계절 지수 평활 모형은 yt = mt + s(t) + at입니다.
평활 방정식은 a 및 d 평활 가중치를 사용하여 다음과 같이 정의됩니다.
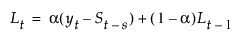
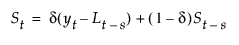
이 모형은 계절 ARIMA(0, 1, s+1)(0, 1, 0)s 모형과 동일합니다.
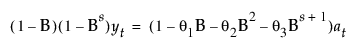
다음은 각 요소에 대한 설명입니다.
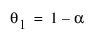
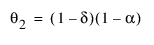
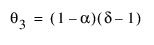
모형의 이동 평균 형식은 다음과 같이 정의됩니다.
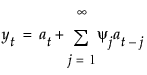 여기서,
여기서, 
Winters 방법(가법 모형)
Winters 방법의 가법 버전 모형은 yt = mt + btt + s(t) + at입니다.
평활 방정식은 a, g 및 d 가중치를 사용하여 다음과 같이 정의됩니다.
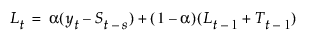
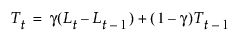
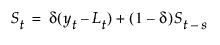
이 모형은 다음과 같이 정의된 계절 ARIMA(0, 1, s+1)(0, 1, 0)s 모형과 동일합니다.
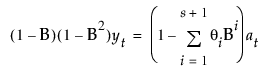
모형의 이동 평균 형식은 다음과 같이 정의됩니다.
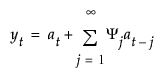
여기서,