개별 관측값에 대한 통계 상세 정보
다변량 관리도 플랫폼을 사용하여 개별 관측값 또는 부분군으로 묶지 않은 측정값을 분석할 수 있습니다. 이러한 측정값 유형의 경우 자연적 부분군 크기는 n = 1입니다. 관측값 수를 m으로 나타내고 측정된 변수의 수를 p로 나타냅니다. 각 관측값에 대한 T2 통계량이 계산되어 그림에 표시됩니다. T2 통계량 및 UCL(관리 상한) 계산은 목표 통계량의 소스에 따라 달라집니다. 단계 I 차트의 한계는 관리도에 표시되는 것과 동일한 데이터를 기반으로 합니다. 단계 II 차트의 한계는 과거 데이터 집합에서 계산된 목표 통계량을 기반으로 합니다. Hotelling T2 관리도의 T2 통계량 및 관리 한계 계산에 대한 자세한 내용은 Montgomery 연구 자료(2013)에서 확인하십시오.
단계 I 관리도에 대한 계산
단계 I 관리도에서 i번째 관측값의 T2 통계량은 다음과 같이 정의됩니다.
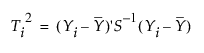
다음은 각 요소에 대한 설명입니다.
Yi = i번째 관측값에 대한 p개 측정값의 열 벡터
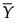= p개 변수에 대한 표본 평균의 열 벡터
S-1 = 표본 공분산 행렬의 역
i개의 각 관측값에 대한 Ti2 값은 다변량 관리도에 표시된 점입니다.
단계 I 관리 한계를 계산할 때 UCL은 베타 분포를 기반으로 합니다. UCL(관리 상한)은 다음과 같이 정의됩니다.
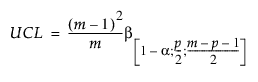
다음은 각 요소에 대한 설명입니다.
p = 변수 수
m = 관측값 수
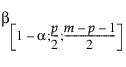= 베타 
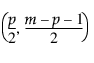분포의 (1–a)번째 분위수
단계 II 관리도에 대한 계산
단계 II 관리도에서 과거 데이터 집합을 X로 정의합니다. 그러면 i번째 관측값의 T2 통계량이 다음과 같이 정의됩니다.
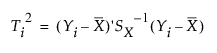
다음은 각 요소에 대한 설명입니다.
Yi = i번째 관측값에 대한 p개 측정값의 열 벡터
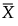= 과거 데이터 집합에서 계산된 p개 변수에 대한 표본 평균의 열 벡터
SX-1 = 과거 데이터 집합에서 계산된 표본 공분산 행렬의 역
i개의 각 관측값에 대한 Ti2 값은 다변량 관리도에 표시된 점입니다.
단계 II 관리 한계를 계산할 때 새 관측값은 과거 데이터 집합과 독립적입니다. 이 경우 UCL(관리 상한)은 F 분포의 함수이며, 목표값을 계산하는 과거 데이터 집합의 관측값 수에 따라 부분적으로 달라집니다. UCL은 다음과 같이 정의됩니다.
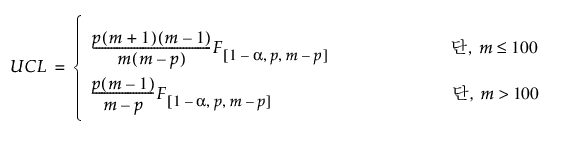
다음은 각 요소에 대한 설명입니다.
p = 변수 수
m = 과거 데이터 집합의 관측값 수
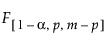= F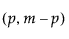
분포의 (1–a)번째 분위수