모니터링 통계량에 대한 통계 상세 정보
이 섹션에는 모형 기반 다변량 관리도 플랫폼의 모니터링 통계량에 대한 계산이 포함되어 있습니다.
T2
i개 관측값 각각의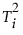 
값이 T2 관리도에 표시됩니다. 과거 및 현재 데이터에 대해 k개의 성분이 있는 PCA 또는 PLS 모형의 T2 값은 다음과 같이 정의됩니다.
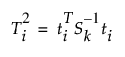
다음은 각 요소에 대한 설명입니다.
ti = i번째 관측값에 대한 k개 스코어의 벡터
Sk = 과거 관측값에 대한 k개 스코어의 대각 표본 공분산 행렬
PCA 모형의 경우 Sk는 대각 고유값 행렬입니다.
데이터 전처리 단계에서 데이터가 중심화되는 경우 k개 과거 스코어 벡터의 평균은 각각 0입니다. 이 단계는 PCA에서 상관계수 행렬 또는 공분산 행렬을 이용하거나, PLS에서 중심화와 함께 발생합니다. X가 중심화되지 않은 전처리 옵션의 경우 데이터가 사용자에 의해 중심화되었다고 가정하므로 k개 스코어 벡터의 평균은 각각 0입니다. Hotelling T2에 대한 자세한 내용은 Montgomery 연구 자료(2013)에서 확인하십시오.
SPE
PCA 모형과 PLS 모형 둘 다 전처리된 X 행렬을 다음과 같이 분해할 수 있습니다.
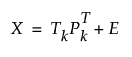
여기서 Tk = (t1,...,tk)는 k차원 스코어 행렬이고, Pk = (p1,...,pk)는 첫 번째 k 고유 벡터가 있는 행렬(PCA 모형의 경우) 또는 적재 행렬(PLS 모형의 경우)입니다. 이 PCA 또는 PLS 모형의 제곱 예측 오차는 SPE 관리도에 사용됩니다.
i개 관측값 각각의 SPEi 값이 SPE 관리도에 표시됩니다. 제곱 예측 오차는 다음과 같이 정의됩니다.
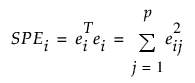
다음은 각 요소에 대한 설명입니다.
ei = 관측값 i에 대한 잔차 벡터
p = 변수 수
DModX
i개 관측값 각각의 DModXi 값이 DModX 관리도에 표시됩니다. 정규화된 DModX(모형까지의 거리)는 다음과 같이 정의됩니다.
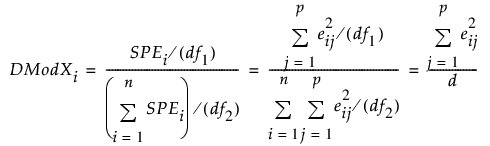
다음은 각 요소에 대한 설명입니다.
eij = 관측값 i와 변수 j에 대한 잔차
df1 = p−k
df2 = 데이터가 중심화된 경우 (n−k−1)(p−k), 데이터가 중심화되지 않은 경우 (n−k)(p−k)
n = 과거 데이터 관측값 수
k = PCA/PLS 성분 수
p = 변수 수
참고: DModXi는 1/d로 척도화된 SPEi와 같습니다.