다변량 검정에 대한 통계 상세 정보

아래에서 E는 잔차 교차곱 행렬이고, H는 모형 교차곱 행렬입니다. E의 대각 요소는 각 변수의 잔차 제곱합입니다. H의 대각 요소는 각 변수에 대한 모형의 제곱합입니다. 판별 분석 관련 문헌에서는 종종 E를 W라고 합니다(W는 within을 나타냄).

다변량 결과 표의 검정 통계량은 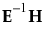의 고유값 l를 사용해서 구합니다. 다음 목록에서는 각 검정 통계량의 계산 방법을 설명합니다.

참고: 반응 설계가 지정된 후 초기 E 및 H 행렬의 앞에 M¢를 곱하고 뒤에 M을 곱합니다.

• Wilks 람다

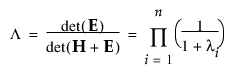
• Pillai 대각합

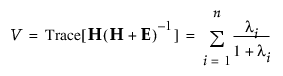
• Hotelling-Lawley 대각합

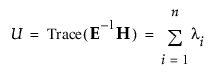
• Roy 최대근

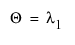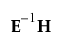, 의 최대 고유값

E 와 H는 다음과 같이 정의됩니다.

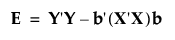
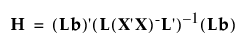
여기서 b는 모형 계수의 추정 벡터이며, A는 행렬 A의 일반화 역행렬을 나타냅니다.

전체 모형 L은 0(절편 값)으로 구성된 열로, 행 및 열 개수가 모형의 모수 개수와 같은 단위 행렬과 연결되어 있습니다. 효과에 대한 L 행렬은 전체 모형 L 행렬의 일부 행으로 구성한 부분집합입니다.

더 많은 정보를 원하십니까? 질문이 있습니까? JMP 사용자 커뮤니티에서 답변 받기 (community.jmp.com).