경사하강법 알고리즘에 대한 통계 상세 정보

t-SNE 방법에 사용되는 Kullback-Leibler 발산은 Barnes-Hut 근사에 기반한 경사하강법 알고리즘을 사용하여 최소화됩니다(van der Maaten, 2014 참조). 이 알고리즘에서는 다음과 같은 표기를 사용합니다.

X = {x1, x2,..., xn} n개의 데이터 점이 있는 원래 고차원 데이터

p = 혼란도 모수

T = 반복 수

h = 학습률

tinflate = 모멘텀 값이 변경되는 최대 반복 수

a(t) = 반복 t에서의 모멘텀, 여기서 t £ tinflate의 경우 a(t) = 0.5이고 그렇지 않은 경우 a(t) = 0.8

Y(t) = {y1, y2,..., yn} 반복 t에서의 저차원 매핑 해

경사하강법 알고리즘의 단계는 다음과 같이 정의됩니다.

1. 고차원 공간의 쌍별 유사성 pj|i를 계산합니다. 지정된 혼란도 p를 기반으로 si를 선택합니다.

2. pij를 계산합니다.

3. 평균이 0이고 표준편차가 10-4인 정규 분포에서 생성되는 초기 해 Y(0) = {y1, y2,..., yn}을 설정합니다.

4. t = 1 ~ T에 대해

– 저차원 매핑의 쌍별 유사성 qij를 계산합니다.

– 비용 함수를 계산합니다.

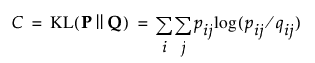
– Barnes-Hut 근사를 사용하여 기울기 함수를 계산합니다.

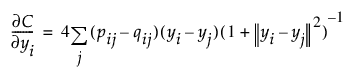
– 해를 업데이트합니다.

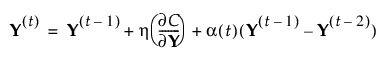
다음 조건 중 하나가 충족되면 알고리즘이 중지됩니다.

• i에 대한 최대 기울기 값이 시작 창에 지정된 수렴 기준보다 작은 경우

• 최대 반복 수 T에 도달한 경우

더 많은 정보를 원하십니까? 질문이 있습니까? JMP 사용자 커뮤니티에서 답변 받기 (community.jmp.com).