오분류 확률에 대한 통계 상세 정보
이 섹션에서는 계량형 차트 플랫폼의 오분류 확률 보고서에 제공되는 확률 계산에 대해 설명합니다. 오분류 확률은 Y(측정된 부품 값)와 X(실제 부품 값)의 결합 확률 함수를 기반으로 합니다. 결합 확률 분포 함수 FYX(y, x)는 평균 벡터 [m, m]과 다음 공분산 행렬이 있는 이변량 정규 분포를 사용합니다.
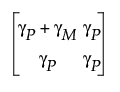
여기서 gP는 부품 간 변동, gM은 측정 변동, m는 총 평균을 나타냅니다. 이러한 통계량은 보고서 창의 통계량에서 찾거나 파생될 수 있습니다. 구체적으로 gP + gM은 TV(총 변동)를 6으로 나눈 값의 제곱, 즉 (TV/6)2과 같고, gP는 PV(부품 변동)를 6으로 나눈 값의 제곱, 즉 (PV/6)2과 같습니다. Y와 X 간의 상관 rYX는 gP/(gP + gM)의 제곱근으로 정의됩니다.
이제 다음 확률을 정의합니다.
d = P[(LSL £ X £ USL) 및 (Y < LSL 또는 Y > USL)]
b = P[(X < LSL 또는 X > USL) 및 (LSL £ Y £ USL)]
p = P(LSL £ X £ USL)
이러한 확률은 결합 확률 분포 함수인 FYX(y, x)와 Y 및 X에 대한 주변 확률 분포 함수인 FY(y) 및 FX(x)로 표현할 수 있습니다.
d = FYX(LSL, USL) - FYX(LSL, LSL) - FYX(USL, USL) + FYX(USL, LSL) + FX(USL) - FX(LSL)
b = FYX(USL, LSL) - FYX(LSL, LSL) - FYX(USL, USL) + FYX(LSL, USL) + FY(USL) - FY(LSL)
p = FX(USL) - FX(LSL)
P(적합한 부품이 잘못 기각됨) = d/p
P(잘못된 부품이 잘못 채택됨) = b/(1-p)
P(부품이 적합하며 기각됨) = d
P(부품이 잘못되었으며 채택됨) = b
P(부품이 적합함) = p