분포 파라미터화에 대한 통계 상세 정보

이 섹션에서는 공정 능력 플랫폼에 사용되는 분포에 대한 밀도 함수 f를 제공합니다. Johnson 및 SHASH 분포를 제외한 모든 분포에 대한 기대값과 분산도 제공합니다.

정규

, , ,

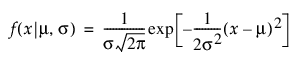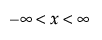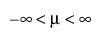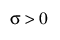
E(x) = m

Var(x) = s2

베타

, , ,

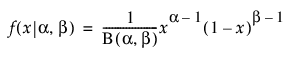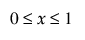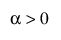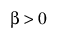
E(x) =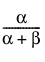

Var(x) =

여기서 B(·)는 베타 함수입니다.

지수

, ,

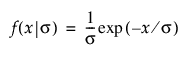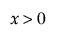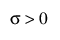
E(x) = s

Var(x) = s2

감마

, , ,

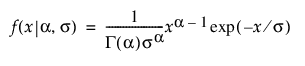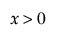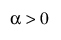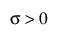
E(x) = as

Var(x) = as2

여기서 G(·)는 감마 함수입니다.

Johnson

Johnson Su

, , ,

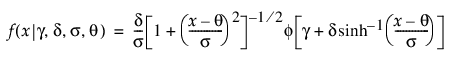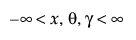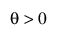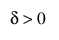
Johnson Sb

, ,

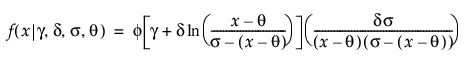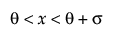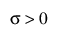
Johnson Sl

, ,

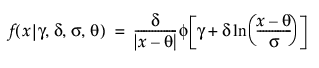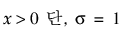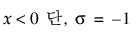
여기서 f(·)는 표준 정규 확률 밀도 함수입니다.

로그 정규

, , ,

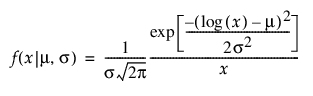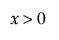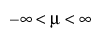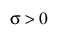
E(x) =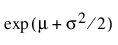

Var(x) =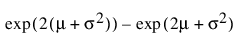

정규 혼합

2 정규 혼합 및 3 정규 혼합 분포 옵션은 다음 파라미터화를 공유합니다.

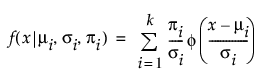
E(x) =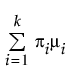

Var(x) =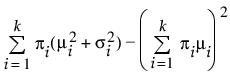

여기서 mi, si 및 pi는 각각 i번째 그룹의 평균, 표준편차 및 비율이며, f(·)는 표준 정규 확률 밀도 함수입니다. 2 정규 혼합의 경우 k는 2입니다. 3 정규 분포 혼합의 경우 k는 3입니다. 혼합물 내 각 그룹에 대해 평균, 표준편차 및 전체 대비 비율이 개별적으로 추정됩니다.

SHASH

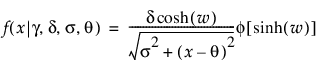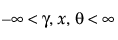, , 0 < d, 0 < s

다음은 각 요소에 대한 설명입니다.

f(·) = 표준 정규 pdf

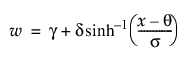
참고: g = 0이고 d = 1인 경우 SHASH 분포는 위치가 q이고 척도가 s인 정규 분포와 동등합니다.

Weibull

, ,

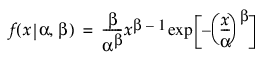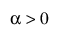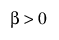
E(x) =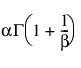

Var(x) =

여기서 G(·)는 감마 함수입니다.

더 많은 정보를 원하십니까? 질문이 있습니까? JMP 사용자 커뮤니티에서 답변 받기 (community.jmp.com).