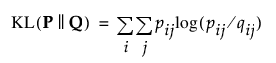t-SNE 방법에 대한 통계 상세 정보
t-SNE 방법은 {xi, xj}의 고차원 유사성과 {yi, yj}의 저차원 유사성 간 차이를 최소화하여 고차원 공간의 점 {x1, x2,..., xn}을 저차원 공간의 점 {y1, y2,..., yn}에 매핑합니다. 쌍별 유사성은 확률 분포로 나타냅니다. 고차원 공간에서 조건부 확률 pj|i는 가우시안 분포를 사용하여 계산됩니다. 다변량 임베딩 플랫폼에서는 조건부 확률을 계산하는 두 가지 방법을 제공합니다.
조건부 확률에 대한 희소 근사 계산
시작 창에서 "희소" 옵션을 선택하는 경우 희소 근사를 사용하여 pj|i가 계산됩니다. n개의 각 입력에 대해 VP(Vantage-Point, 기준점) 트리를 사용하여 최근접 이웃 집합이 발견됩니다. 그런 다음 최근접 이웃의 부분집합에 대해서만 조건부 확률이 계산됩니다.
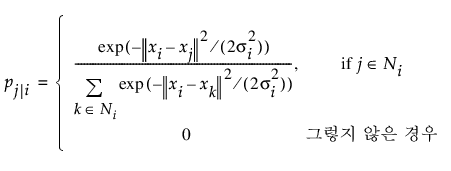
이 방정식에서 Ni는 xi의 floor(3p) 최근접 이웃 집합입니다. 여기서 p는 시작 창에 정의된 혼란도 모수입니다. 가우시안 분포의 분산 si도 혼란도 모수를 기반으로 합니다. 자세한 내용은 van der Maaten & Hinton(2008) 및 van der Maaten(2014)에서 확인하십시오.
조건부 확률에 대한 비희소 계산
시작 창에서 "희소" 옵션을 선택하지 않는 경우 모든 점에 대해 pj|i가 계산됩니다.
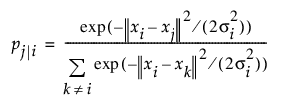
이 계산에서 가우시안 분포의 분산 si도 혼란도 모수를 기반으로 합니다.
결합 확률 분포 계산
t-SNE 방법에서는 조건부 확률이 대칭이라고 가정합니다. 따라서 고차원 공간에서 결합 확률 pij는 다음과 같이 대칭 조건부 유사성에 의해 정의됩니다.
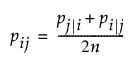
이때 모든 i와 j에 대해 pij = pji입니다. 쌍별 유사성에 관심이 있으므로 pii = 0도 가정됩니다.
저차원 매핑의 결합 확률 qij는 자유도가 1인 스튜던트 t 분포를 사용하여 계산됩니다.
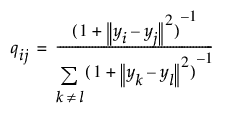
이러한 확률은 pij와 동일한 특성을 갖습니다. 즉, 모든 i와 j에 대해 qij = qji이고 qii = 0입니다.
t-SNE 방법은 결합 확률 분포 P와 결합 확률 분포 Q 사이의 단일 Kullback-Leibler 발산을 최소화하여 고차원 공간의 쌍별 유사성과 저차원 공간의 쌍별 유사성 간 차이를 최소화합니다. P와 Q 사이의 Kullback-Leibler 발산은 다음과 같이 계산됩니다.
