V-마스크 CUSUM 관리도에 대한 통계 상세 정보
이러한 계산식에는 다음 표기가 사용됩니다.
• m는 모집단의 평균을 나타내며 공정 평균 또는 공정 수준이라고도 합니다.
• m0은 모집단의 목표 평균(목표)을 나타냅니다. 경우에 따라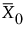 
기호가 m0에 사용됩니다. 자세한 내용은 American Society for Quality Statistics Division(2004)에서 확인하십시오. 시작 창의 "CUSUM 차트에 대한 알려진 통계" 영역에서 m0을 "목표값"으로 제공할 수 있습니다.
• s는 모집단 표준편차를 나타내고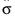 
는 s의 추정값을 나타냅니다.
• s0은 알려진 표준편차를 나타냅니다. 시작 창의 "CUSUM 차트에 대한 알려진 통계" 영역에서 so을 "시그마"로 제공할 수 있습니다.
• n은 CUSUM 차트의 명목형 표본 크기를 나타냅니다.
• d는 감지할 m 변화를 나타내며, 표준편차의 배수로 표현됩니다. 시작 창의 "CUSUM 차트에 대한 알려진 통계" 영역에서 d를 "델타"로 제공할 수 있습니다.
• D는 감지할 m 변화를 나타내며, 데이터 단위로 표현됩니다. 전체 부분군에서 표본 크기 n이 일정하면 다음 계산이 적용됩니다.
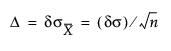
시작 창의 "CUSUM 차트에 대한 알려진 통계" 영역에서 D를 "변화"로 제공할 수 있습니다.
참고: 일부 작성자는 D 대신 D 기호를 사용합니다.
단측 CUSUM 차트
양의 변화
감지할 변화(d)가 양수이면 t번째 부분군의 CUSUM이 다음과 같이 계산됩니다.
St = max(0, St – 1+ (zt – k))
t = 1, 2,..., n. 여기서 S0 = 0이고 zt는 양측 차트에 대해 정의됩니다. 참조 값이라고 하는 k 모수는 양수입니다. 시작 창에서 k 모수가 지정되지 않은 경우 k는 d/2로 설정됩니다. CUSUM St를 상위 누적합이라고 합니다. St는 다음과 같이 계산할 수 있습니다.
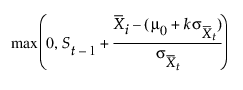
St 수열은 m0으로부터 k 표준 오차보다 큰 부분군 평균의 편차를 누적합니다. St가 양수 값 h(결정 구간이라고 함)를 초과하면 변화 또는 관리이탈 상태 신호가 표시됩니다.
음의 변화
감지할 변화가 음수이면 t번째 부분군의 CUSUM이 다음과 같이 계산됩니다.
St = max(0, St – 1 – (zt + k))
t = 1, 2,..., n. 여기서 S0 = 0이고 zt는 양측 차트에 대해 정의됩니다. 참조 값이라고 하는 k 모수는 양수입니다. 시작 창에서 k 모수가 지정되지 않은 경우 k는 d/2로 설정됩니다. CUSUM St를 하위 누적합이라고 합니다. St는 다음과 같이 계산할 수 있습니다.
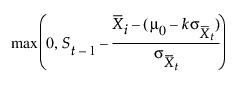
St 수열은 m0으로부터 k 표준 오차보다 작은 부분군 평균의 편차 절대값을 누적합니다. St가 양수 값 h(결정 구간이라고 함)를 초과하면 변화 또는 관리이탈 상태 신호가 표시됩니다.
d가 양수 또는 음수인지에 관계없이 St는 항상 양수이고 h도 항상 양수입니다. 음의 변화를 감지하기 위한 차트의 경우 일부 작성자는 St가 음수 한계보다 작을 때 변화 신호가 발생하는 St의 반사형 버전을 정의합니다.
Lucas and Crosier(1982)에서는 초기 CUSUM S0이 "시작값"으로 설정된 CUSUM 차트에 대한 FIR(Fast Initial Response) 기능의 특성을 설명합니다. 이 차트에서 제공하는 평균 런 길이 계산을 통해 공정이 관리 상태일 때는 FIR 기능이 미치는 효과가 거의 없으며, 결과적으로 초기 관리이탈 상태에 대한 반응이 표준 CUSUM 차트보다 빠르다는 것을 알 수 있습니다. 시작 창의 "CUSUM 차트에 대한 알려진 통계" 영역에서 "시작값"을 제공할 수 있습니다.
상수 표본 크기
부분군 표본 크기가 일정하면(n) 데이터와 동일한 단위로 척도화된 CUSUM을 계산하는 것이 더 좋을 수 있습니다. 이 경우 CUSUM은 다음과 같이 계산됩니다.
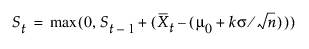
여기서, d > 0
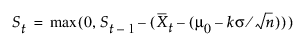
여기서, d < 0입니다. 두 경우 모두 k 모수의 척도가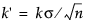 
로 조정됩니다. 시작 창에서 k 모수가 지정되지 않은 경우 k'는 d/2로 설정됩니다. St가 
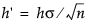를 초과하면 변화 신호가 발생합니다. 일부 작성자는 h'에 H 기호를 사용합니다.
양측 CUSUM 차트
CUSUM 차트가 양측인 경우 t번째 부분군에 대해 표시되는 누적합 St는 다음과 같이 정의됩니다.
St = St - 1 +zt
t = 1, 2,..., n. 여기서 S0=0이고 zt 항은 다음과 같이 계산됩니다.
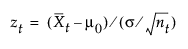
여기서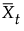 
는 t번째 부분군 평균이고 nt는 t번째 부분군 표본 크기입니다. 부분군 표본이 개별 측정값 xt로 구성된 경우 zt 항 계산은 다음과 같이 단순화됩니다.
zt = (xt – m0)/s
첫 번째 방정식은 다음과 같이 다시 쓸 수 있습니다.
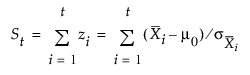
여기서 St 수열은 목표 평균 m0과 부분군 평균 간의 표준화된 편차를 누적합니다.
대부분의 경우 부분군 표본 크기 ni는 일정하고(ni = n) St에 대한 방정식은 다음과 같이 단순화될 수 있습니다.
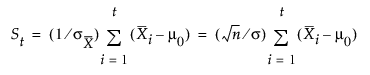
경우에 따라 St를 다음과 같이 계산하는 것이 더 좋을 수 있습니다.
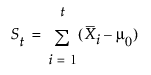
이렇게 하면 데이터와 동일한 단위로 척도화됩니다. 이 경우 V-마스크 모수 h와 k는 각각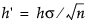 
및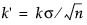 
로 척도가 조정됩니다. 일부 작성자는 k'에 F 기호를 사용하고 h'에 H 기호를 사용합니다.
공정이 관리 상태이고 평균 m가 목표값 m0이거나 이 값에 가까우면 확률 보행 모형이 적용됩니다. 따라서 점이 0에서 멀어질 수 있지만 m0에서부터 양의 이동과 음의 이동은 서로 상쇄되는 경향이 있으므로 큰 추세를 보이지는 않습니다. m가 양의 방향으로 이동하면 점이 상향 추세를 나타내고 m가 음의 방향으로 이동하면 점이 하향 추세를 나타냅니다.