초월함수
JMP 계산식 편집기에서 밑에 대한 로그 함수, 조합 계산을 위한 함수, 베타 함수 및 일부 감마 함수와 같은 초월함수를 지원하는 계산식을 생성할 수 있습니다. 구문에 대한 자세한 내용은 Scripting Guide의 “Transcendental Functions”에서 확인하십시오.
Exp
e를 지정한 횟수만큼 거듭제곱합니다. 따라서 Exp(1) = e입니다.
ExpM1
x가 매우 작을 경우 Exp(x) - 1에 대한 더 정확한 계산을 반환합니다.
Ln
x의 자연 로그를 계산합니다.
Log 및 Log10
e를 밑으로 하는 자연 로그를 계산합니다. 기본 밑을 변경하려면 인수를 강조 표시하고 쉼표를 입력하거나 계산식 편집기 키패드의 삽입 키를 클릭하십시오. 그러면 밑이 표시되며 이를 편집할 수 있습니다. Log 인수는 임의의 숫자 표현식일 수 있습니다. 표현식 Log(e)의 결과는 1이 되고, Log(32,2)의 결과는 5가 됩니다. Log10 함수는 상용 로그만 계산합니다.
Log1P
x가 매우 작을 경우 Log(1+x)에 대한 더 정확한 계산을 반환합니다.
Squash
함수 1 / (1 + ex)를 계산합니다. 여기서 x는 숫자 열, 변수 또는 표현식입니다.
Logist
Squish 또는 Logistic이라고도 하며, 함수 1 / (1+e-x)를 효율적으로 계산하는 방법입니다. 여기서 x는 숫자 열, 변수 또는 표현식입니다.
Root(Square Root)
인덱스로 지정된 인수의 제곱근을 계산합니다. Root는 기본적으로 인덱스 2와 함께 표시됩니다. 인덱스를 변경하려면 인덱스 인수를 강조 표시하고 원하는 값을 입력하십시오.
Factorial
1부터 지정한 인수까지 모든 수를 곱한 결과를 반환합니다. 예를 들어 Factorial(5)의 결과는 120이 됩니다.
NChooseK
n개의 항목 중 한 번에 k개를 선택하는 경우의 수(n select k)를 반환하며, 계승을 사용하는 표준 방법, 즉 n! / (k!(n – k)!)로 계산됩니다. 예를 들어 NChooseK(5,2)의 결과는 10이 됩니다.
베타
2모수 Beta 함수를 추가하며, Gamma 함수로는 다음과 같이 작성됩니다.
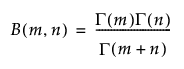
감마
G(i)로 나타내는 Gamma 함수를 추가하며, 다음과 같이 정의됩니다.
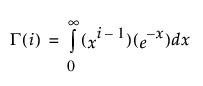
단일 인수를 사용하는 Gamma는 Gamma(x, infinity)와 동일합니다. 선택적인 두 번째 인수는 상한 정수를 무한대에서 사용자가 입력한 값으로 변경합니다. 다른 흥미로운 감마 함수 관계식은 다음과 같습니다.
• 1보다 큰 임의의 a에 대해, G(a) = (a–1) • G(a–1)
• 임의의 양의 정수에 대해, n, G(n) = (n-1)!
• G(0.5) = p의 제곱근
LGamma
감마 함수 계산 결과의 자연 로그입니다. Log(자연 로그) 함수와 Gamma 함수를 함께 사용할 때와 동일한 결과가 반환됩니다. 하지만 LGamma 함수를 사용한 계산이 Log(자연 로그) 및 Gamma 함수를 함께 사용한 계산보다 더 효율적입니다. NChooseK는 LGamma 함수를 사용하여 구현됩니다. 결과가 항상 정확한 정수가 되지는 않습니다. 결과가 정수에 가까우면 Floor 함수를 사용하여 올림됩니다.
Digamma
Gamma 함수의 로그 도함수입니다.
Trigamma
Digamma 함수의 도함수, 또는 Gamma 함수의 로그 2차 도함수입니다.
Arrhenius
아레니우스 관계식의 비특정 성분을 계산한 다음 아레니우스 방정식의 활성화 에너지로 곱합니다.
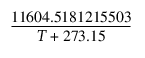
Arrhenius Inv
Arrhenius 함수의 역함수를 반환합니다.
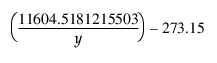
Logit
다음을 사용하여 인수에 로짓 변환을 적용합니다.
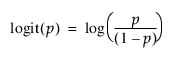
Logit Percent
인수에 대한 로짓 백분율을 계산합니다.
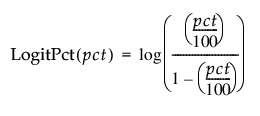
Logist Percent
인수에 대한 로지스틱 백분율을 계산합니다.
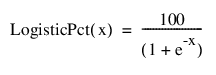
Scheffe Cubic
특정 모형의 적합에 사용됩니다. Scheffe Cubic (X1, X2)는 X1*X2*(X1-X2)와 동등합니다.
SbInv
Johnson Sb 역 변환입니다. 인수가 정규 분포를 따를 경우 결과는 Johnson Sb입니다.
SbTrans
이중 경계 변수에서 표준 정규(0, 1) 분포로의 Johnson Sb 변환입니다.
SHASHInv
표준 정규 분포를 따르는 변수를 SHASH(SinH-ArcSinH) 분포를 따르는 변수로 변환한 결과를 반환합니다.
SHASHTrans
SHASH(SinH-ArcSinH) 분포를 따르는 변수를 표준 정규 분포를 따르는 변수로 변환한 결과를 반환합니다.
SlInv
Johnson Sl 역 변환입니다. 인수가 정규 분포를 따를 경우 결과는 Johnson Sl입니다.
SlTrans
이중 경계 변수에서 표준 정규(0, 1) 분포로의 Johnson Sl 변환입니다.
SuInv
Johnson Su 역 변환입니다. 인수가 정규 분포를 따를 경우 결과는 Johnson Su입니다.
SuTrans
이중 경계 변수에서 표준 정규(0, 1) 분포로의 Johnson Su 변환입니다.