多项式效应模型的示例

使用“拟合模型”平台的“标准最小二乘法”特质拟合二元数据的三次多项式模型。

1. 选择帮助 > 样本数据文件夹，然后打开 Growth.jmp。

2. 选择分析 > 拟合模型。

3. 选择比率并点击 Y。

4. 在次数旁边的文本框中键入 3。

5. 选择年龄并点击宏 > 多项式次数。

这会向模型中添加三个项。

6. 点击运行。

下面显示报表各个部分及说明。

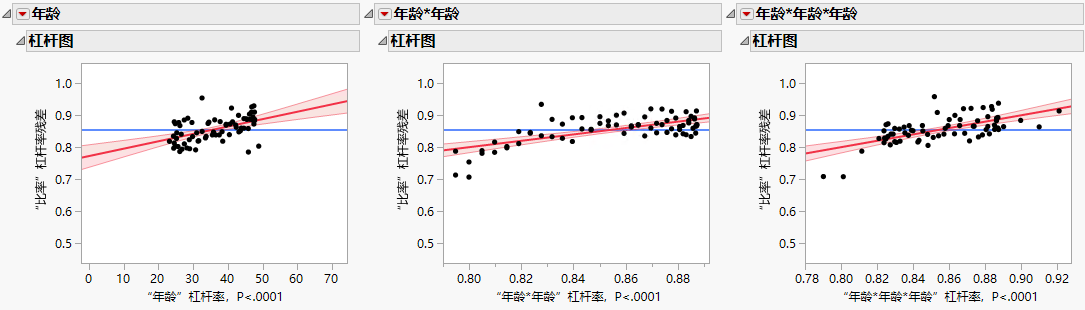
杠杆图

使用杠杆图来确定有影响的观测，并评估其对回归模型的影响。

图 4.2 杠杆图 

杠杆图没有显示任何有影响的数据点，模型中的所有变量都是显著的。

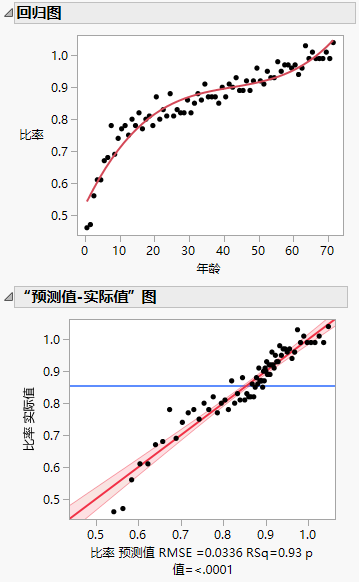
回归图和“预测值-实际值”图

使用回归图和“预测值-实际值”图可评估模型的性能和准确度。

图 4.3 回归图和“预测值-实际值”图 

“回归图”显示数据点和数据的非线性（三次多项式）回归模型拟合。“预测值-实际值”图中的点跟随 y = x 这条线，这表明模型预测很接近实际值。

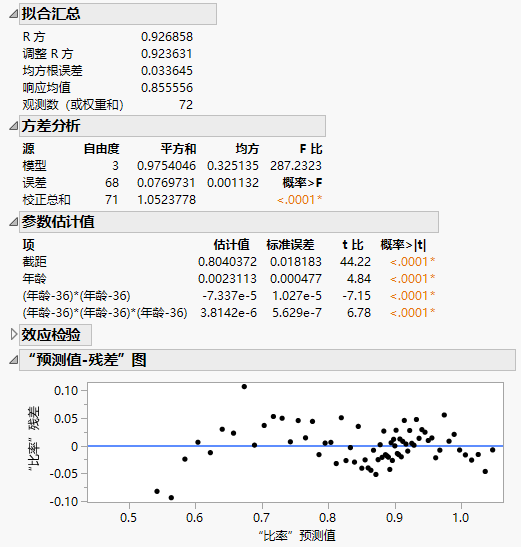
模型拟合汇总表和残差图

使用报表中的表来评估模型拟合和响应变量统计量。“拟合汇总”表包含用于评估模型拟合和响应变量统计量的信息。“方差分析”表包含有关总体模型显著性和变异来源的信息。“参数估计值”表包含系数、标准误差和预测变量显著性。“效应检验”表包含有关各预测变量的显著性的信息。“预测值-残差”图是通过检查预测值范围内残差的模式或趋势来评估回归模型的假设和性能。

图 4.4 回归模型汇总和残差分析 

在本例中，“方差分析”表和“参数估计值”表分别表明该模型在统计上是显著的，并且该模型中包括的变量的所有系数在统计上都是显著的。同样，“拟合汇总”表显示有较高的 R 方值 0.927，这指示预测变量和响应变量之间有很强的关系。

“预测值-残差”图显示残差在零线上下随机分散且均匀分布。这表明满足了模型假设且残差正态分布。

需要更多信息？有问题？从 JMP 用户社区得到解答 (community.jmp.com).