包含交互作用的双因子方差分析的示例
使用“拟合模型”平台的“标准最小二乘法”特质拟合包含交互作用项的双因子方差分析模型。您关注爆米花的类型和包型大小是否对爆米花产量有影响。
1. 选择帮助 > 样本数据文件夹,然后打开 Popcorn.jmp。
2. 选择分析 > 拟合模型。
3. 选择产量并点击 Y。
4. 选择爆米花和包型,然后点击宏 > 完全析因。
5. 点击运行。
6. 点击“响应‘产量’”红色小三角并选择因子刻画 > 刻画器。
下面显示报表各个部分及说明。
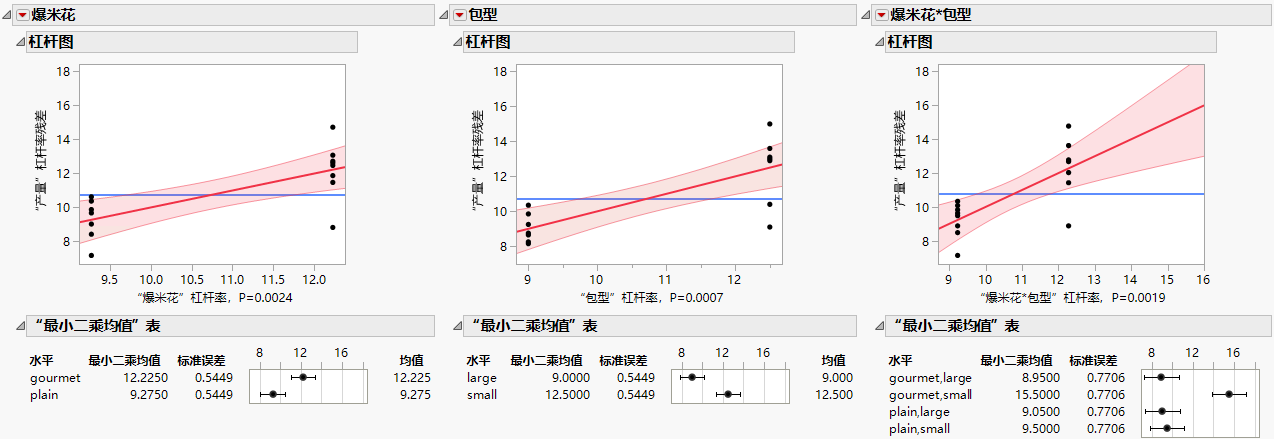
杠杆图
使用杠杆图来确定有影响的观测,并评估其对回归模型的影响。
图 4.12 因子及其交互作用的“杠杆图”和“最小二乘均值”表
您观察到,爆米花的类型和包型的大小之间存在较强的交互作用效应,如交互作用效应的杠杆图中这条线的斜率所示。
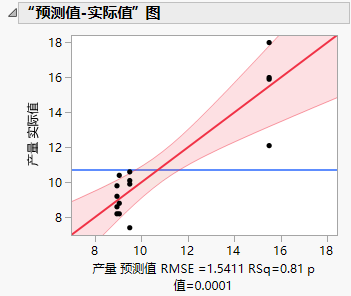
“预测值-实际值”图
使用“预测值-实际值”图可通过比较疼痛响应的实际值与模型中的预测值,来评估模型的性能和准确度。
图 4.13 “预测值-实际值”图
观测到实际值与预测值之间的关系在统计学上是显著的(p 值 = 0.0001)。
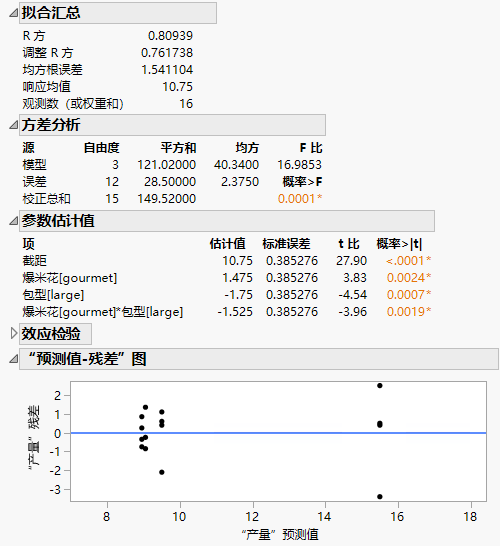
模型拟合汇总表和残差图
使用报表中的表来评估模型拟合和响应变量统计量。“拟合汇总”表包含用于评估模型拟合和响应变量统计量的信息。“方差分析”表包含有关总体模型显著性和变异来源的信息。“参数估计值”表包含系数、标准误差和预测变量显著性。“效应检验”表包含有关各预测变量的显著性的信息。“预测值-残差”图是通过检查预测值范围内残差的模式或趋势来评估回归模型的假设和性能。
图 4.14 包含方差分析、参数和残差的模型汇总
观测到回归模型的 R 方统计量为 0.809,p 值为 0.0001,这两者均支持模型的值。这两个因子及其交互作用都具有显著的效应,如系数为零的检验的 p 值所测量的那样。
“预测值-残差”图显示残差在零线上下随机分散且均匀分布。这表明满足了模型假设且残差正态分布。
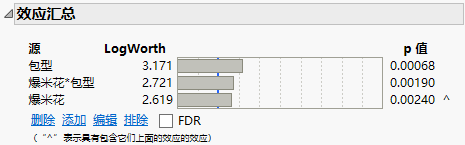
效应汇总
使用“效应汇总”表快速评估与响应变量相关的每个因子的关联强度和统计显著性。
图 4.15 “效应汇总”表
三个因子全都显示出较高的 Logworth 值和极小的 p 值,这表明它们对响应变量影响显著。
预测刻画器
使用“预测刻画器”探索响应的预测值是如何根据因子设置而变化的。
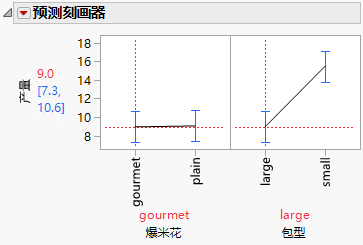
图 4.16 预测刻画器
采用较大包型的 gourmet 爆米花的预测产量响应为 9.0,95% 置信区间为 7.3 到 10.6。您可以在“预测刻画器”中以交互方式探索爆米花和包型水平的各种组合的产量。有关使用“预测刻画器”解释模型的详细信息,请参见双因子方差分析的示例。