估计方法的统计详细信息
在“拟合模型”平台的“广义回归”特质中，估计方法包括惩罚回归方法，这些方法通过赋予回归系数罚值给回归系数引入了偏倚。
岭回归
岭回归对回归系数应用 l2 罚值。岭回归系数估计值定义如下：
,
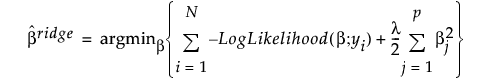其中，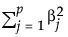
是 l2 罚值，l 是调节参数，N 是行数，p 是变量数。
Dantzig 选择器
“Dantzig 选择器”方法对残差与 X 列的内积应用 l∞ 范数。Dantzig 选择器的系数估计值满足以下准则：
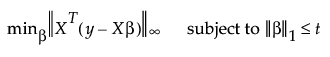
其中，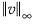
表示 l∞ 范数，
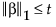是 l1 罚值，t 是调节参数。l∞ 范数是向量 v 的分量的最大绝对值。
Lasso 回归
Lasso 方法对回归系数应用 l1 罚值。Lasso 的系数估计值定义如下：
,
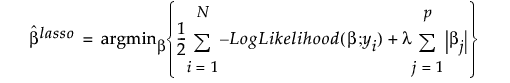其中，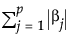
是 l1 罚值，l 是调节参数，N 是行数，p 是变量数
弹性网络
“弹性网络”方法组合 l1 和 l2 罚值。“弹性网络”的系数估计值定义如下：
,
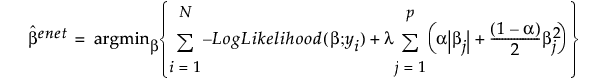这是等式中使用的符号：
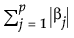是 l1 罚值
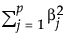是 l2 罚值
l 是调节参数
a 是一个参数，用于确定 l1 和 l2 罚值的组合值
N 是行数
p 是变量数
提示：有两个样本脚本，这两个脚本演示变动单个预测变量的弹性网络中的 a 和 l 的收缩影响。选择帮助 > 样本索引，点击“样本索引”红色小三角，选择“打开样本”>“脚本”，然后选择 demoElasticNetAlphaLambda.jsl 或 demoElasticNetAlphaLambda2.jsl。每个脚本都包含关于使用方法和演示内容的说明。
自适应方法
自适应 Lasso 方法使用加权罚值来提供一致的系数估计值。l1 罚值的加权形式定义如下：
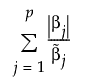
其中，若 MLE 存在，则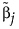 
是 MLE。若 MLE 不存在并且响应分布为正态分布，则使用最小二乘法进行估计，而 
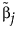是使用广义逆矩阵求得的解。若响应分布非正态分布，则 
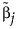是岭解。
对于自适应 Lasso，这个加权形式的 l1 罚值用于确定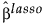 
系数。
自适应弹性网络使用这个加权形式的 l1 罚值，也应用 l2 罚值的加权形式。自适应弹性网络的 l2 罚值的加权形式定义如下：
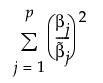
其中，若 MLE 存在，则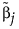 
是 MLE。若 MLE 不存在并且响应分布为正态分布，则使用最小二乘法进行估计，而 
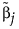是使用广义逆矩阵求得的解。若响应分布非正态分布，则 
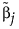是岭解。