外推控制量度的统计详细信息
“预测刻画器”中的“外推控制”选项有两个量度，这些量度用于确定一个点是否为外推。使用的量度类型取决于模型拟合类型。
杠杆率
对于在“拟合模型”平台的“标准最小二乘法”特质中拟合的模型，因子设置的杠杆率用作默认外推量度。
第 i 个观测的杠杆率 hii 是矩阵 X(X′X)-1X′（有时称为帽子矩阵）的第 i 个对角线元素。新预测点的杠杆率计算如下：hpred = x′pred(X′X)-1xpred。以下两个准则可用于确定具有杠杆率 hpred 的预测是否为外推：
• hpred > K × max(hii)，其中 K 是可定制的乘数
• hpred > L × p/n，其中 L 是可定制的乘数，p 是变量数，n 是观测数，p/n 是平均杠杆率
可以使用“设置阈值准则”选项指定使用哪种准则以及乘数的值。默认乘数值为 K = 1 和 L = 3。
注意：从“图形”菜单运行的刻画器上的外推控制若使用保存的最小二乘法模型，则不执行杠杆方法，改为使用“正则 Hotelling T2”方法。
正则 Hotelling T2
在最小二乘法模型之外的模型中，正则 Hotelling T2 值用作默认外推量度。训练数据的 T2 值和预测点的 T2 值计算如下：
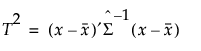
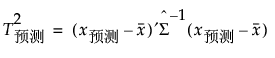
其中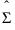 
是对训练数据估计的 Schafer 和 Strimmer 正则协方差矩阵估计量。用于 Schafer Strimmer 估计量的目标矩阵是对角协方差矩阵。请参见 Schafer and Strimmer (2005)。在使用带有缺失值的观测训练模型的平台中，用配对删除来估计协方差矩阵。
注意：在上述计算中，分类变量要转换为指标变量。
阈值的计算取决于根据训练数据计算的非缺失 T2 值的数量。
• 若有十个或更多非缺失 T2 值，则阈值设置如下：
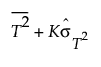
其中
K 是可定制乘数且默认设置为 3
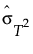是 T2 值的标准差。
• 若非缺失值 T2 不足十个，则使用等价于 Ks 限值的 F 分布分位数来设置阈值。
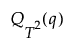
其中
q= F(K)
F(·) 是标准正态分布
K 是可定制乘数且默认设置为 3
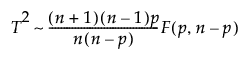
p 是参数个数
r 是非缺失 T2 值的个数
K 最近邻
若将“K 最近邻”选作“外推类型选项”，k 最近邻距离将用于计算外推量度和阈值。该方法使用以下符号。
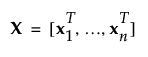= 标准化预测变量的矩阵
xi = 数据中的第 i 个点
n = 观测数
p = 预测变量数
k = 近邻数
d(x, x′) = 两点之间的欧氏距离
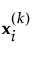= 第 i 个点 xi 的第 k 个最近邻
对于由 x 定义的因子设置，外推量度为 d(x, x(1))。这是由因子设置定义的点与其在数据中的第一个最近邻居之间的距离。该阈值使用以下等式设置：
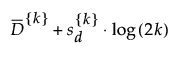
其中
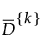是所有点与其 k 个近邻之间的配对距离的均值
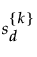是所有点与其 k 个近邻之间的配对距离的标准差。