短期运行控制图的统计详细信息
本节介绍如何在“控制图生成器”中计算短期运行控制图的控制限。请参见 Wise and Fair (2006)。
产品统计量的统计详细信息
“产品统计量”表包含每个产品的目标值和 sigma 值。产品目标值 Tj 是产品 j 中观测的估计均值。产品 sigma sj 是每个产品的估计标准差。使用以下公式计算产品目标值和产品 sigma 值。
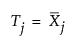
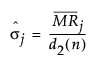
若指定了子组，则使用以下公式计算产品 sigma：
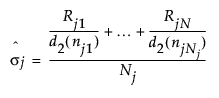
若指定了子组并且子组大小不等，则使用以下公式计算总体未调整 sigma：
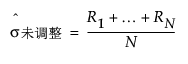
若未指定任何产品/部件变量，总均值和估计标准差如下表所示，并使用以下公式计算：
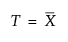
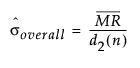
其中：
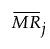= 产品 j 的非缺失移动极差的均值
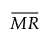= 非缺失移动极差的均值
d2(n) = 服从单位标准差正态分布的 n 个自变量的极差的期望值
nji = 部件 j 的第 i 个子组的样本大小
Rji = 部件 j 的第 i 个子组的极差
Nj 是 nij ≥ 2 的部件 j 中的子组数
Ri = 第 i 个子组的极差
N 是 ni ≥ 2 的子组数。
目标值和 sigma 值用于计算短期运行控制图上的点。对于中心化图，通过减去相应产品的目标值使每个观测中心化。对于标准化图，通过减去相应产品的目标值再除以产品 sigma 值使每个观测标准化。
基于中心化的短期运行差值图和移动极差图的统计详细信息
短期运行差值图的控制限计算如下：
短期运行差值图的下控制限 =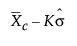 
短期运行差值图的中心线 =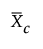 
短期运行差值图的上控制限 =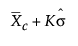 
基于中心化的短期运行移动极差图的控制限计算如下：
基于中心化的短期运行移动极差图的下控制限 = 0
基于中心化的短期运行移动极差图的中心线 =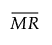 
基于中心化的短期运行移动极差图的上控制限 =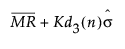 
基于中心化的短期运行差值图和移动极差图的标准差估计如下：
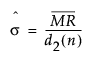
其中：
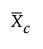= 中心化测量值的均值
K = sigma 乘数，且默认设置为 3
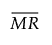= 非缺失移动极差的均值
d2(n) = n 个具有单位标准差的服从独立正态分布的变量的极差的期望值
d3(n) = n 个具有单位标准差的服从独立正态分布的变量的极差的标准差。
注意：“控制图生成器”中的移动极差图使用 n = 2 的极差跨度。
基于标准化的短期运行 Z 图和移动极差图的统计详细信息
短期运行 Z 图的控制限计算如下：
短期运行 Z 图的下控制限 =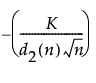 
短期运行 Z 图的中心线 = 0
短期运行 Z 图的上控制限 =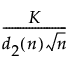 
基于标准化的短期运行移动极差图的控制限计算如下：
基于标准化的短期运行移动极差图的下控制限 =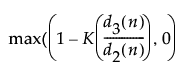 
基于标准化的短期运行移动极差图的中心线 = 1
基于标准化的短期运行移动极差图的上控制限 =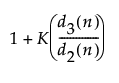 
其中：
K = sigma 乘数，且默认设置为 3
d2(n) = n 个具有单位标准差的服从独立正态分布的变量的极差的期望值
d3(n) = n 个具有单位标准差的服从独立正态分布的变量的极差的标准差。
注意：“控制图生成器”中的移动极差图使用 n = 2 的极差跨度。
基于标准化数据的短期运行 Z 图的中心线为 0，短期运行移动极差图的中心线为 1。
基于中心化的短期运行平均差值图和极差图的统计详细信息
短期运行平均差值图的控制限计算如下：
短期运行平均差值图的下控制限 =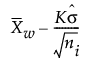 
短期运行平均差值图的中心线 =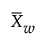 
短期运行平均差值图的上控制限 =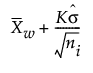 
基于中心化的短期运行极差图的控制限计算如下：
基于中心化的短期运行极差图的下控制限 =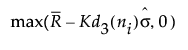 
基于中心化的短期运行极差图的中心线 =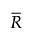 
基于中心化的短期运行极差图的上控制限 =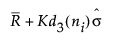 
基于中心化的短期运行差值图和极差图的标准差估计如下：
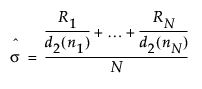
其中：
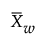= 子组差值的加权平均值
K = sigma 乘数，且默认设置为 3
ni = 第 i 个子组的样本大小
d2(n) 是服从单位标准差正态分布的 n 个自变量的极差的期望值
d3(n) 是服从单位标准差正态分布的 n 个自变量的极差的标准差
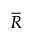= 非缺失极差的均值
Ri 是第 i 个子组的极差
N 是 ni ≥ 2 的子组数。
基于标准化的短期运行 Z 图和极差图的统计详细信息
短期运行 Z 图的控制限计算如下：
短期运行 Z 图的下控制限 =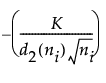 
短期运行 Z 图的中心线 = 0
短期运行 Z 图的上控制限 =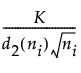 
基于标准化的短期运行极差图的控制限计算如下：
基于标准化的短期运行极差图的下控制限 = D3
基于标准化的短期运行极差图的中心线 = 1
基于标准化的短期运行极差图的上控制限 =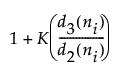 
其中：
K = sigma 乘数，且默认设置为 3
ni = 第 i 个子组的样本大小
d2(n) 是服从单位标准差正态分布的 n 个自变量的极差的期望值
d3(n) 是服从单位标准差正态分布的 n 个自变量的极差的标准差