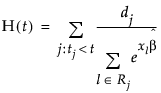比例风险模型是 D. R. Cox (1972) 提出的特殊半参数回归模型,用来检查解释变量对生存时间的影响。假定总体的每个成员的生存时间遵循各自的危险率函数。
比例风险在某种意义上来说是非参数的,因为它涉及未指定的任意基准危险率函数。它又是参数的,因为它采用了协变量的参数形式。基准危险率函数采用与时间无关的协变量模型的函数来统一尺度以给出一般危险率函数。与 Kaplan-Meier 分析不同,比例风险计算每个协变量的参数估计值和标准误差。使用最大似然法估计与解释变量关联的回归参数 (β) 及其标准误差。还从参数估计值计算条件风险比(或危险比)。
使用经验法生成比例风险的生存估计值。请参见 Lawless (1982)。它们表示生存函数 S(t) 的经验累积危险率函数估计值 H(t),可以表示为 S0 = exp(-H(t)),其中危险率函数按以下公式计算: