t = 1, 2,..., n, where S0 = 0, zt is defined as for two-sided charts, and the parameter k, termed the reference value, is positive. If the parameter k is not specified in the launch window, k is set to δ/2. The CUSUM St is referred to as an upper cumulative sum. St can be computed as follows:
The sequence St cumulates deviations in the subgroup means greater than k standard errors from μ0. If St exceeds a positive value h (referred to as the decision interval), a shift or out-of-control condition is signaled.
t = 1, 2,..., n, where S0 = 0, zt is defined as for two-sided charts, and the parameter k, termed the reference value, is positive. If the parameter k is not specified in the launch window, k is set to δ/2. The CUSUM St is referred to as a lower cumulative sum. St can be computed as follows:
The sequence St cumulates the absolute value of deviations in the subgroup means less than k standard errors from μ0. If St exceeds a positive value h (referred to as the decision interval), a shift or out-of-control condition is signaled.
Note that St is always positive and h is always positive, regardless of whether δ is positive or negative. For charts designed to detect a negative shift, some authors define a reflected version of St for which a shift is signaled when St is less than a negative limit.
Lucas and Crosier (1982) describe the properties of a fast initial response (FIR) feature for CUSUM charts in which the initial CUSUM S0 is set to a “head start” value. Average run length calculations given by them show that the FIR feature has little effect when the process is in control and that it leads to a faster response to an initial out-of-control condition than a standard CUSUM chart. You can provide a Head Start value in the Known Statistics for CUSUM Chart area on the launch window.
When the subgroup sample sizes are constant (= n), it might be preferable to compute CUSUMs that are scaled in the same units as the data. CUSUMs are then computed as follows:
where δ > 0
where δ < 0. In either case, the parameter k is rescaled to  . If the parameter k is not specified in the launch window, k' is set to δ/2. A shift is signaled if St exceeds
. If the parameter k is not specified in the launch window, k' is set to δ/2. A shift is signaled if St exceeds 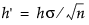 . Some authors use the symbol H for h'.
. Some authors use the symbol H for h'.
 . If the parameter k is not specified in the launch window, k' is set to δ/2. A shift is signaled if St exceeds
. If the parameter k is not specified in the launch window, k' is set to δ/2. A shift is signaled if St exceeds 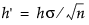 . Some authors use the symbol H for h'.
. Some authors use the symbol H for h'.


