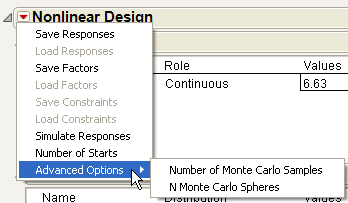
Advanced Options for the Nonlinear Designer

For advanced users, the Nonlinear Designer has the two additional options, as shown in Advanced Options for the Nonlinear Designer. These advanced options are included because finding nonlinear DOE solutions involves minimizing the integral of the log of the determinant of the Fisher information matrix with respect to the prior distribution of the parameters. These integrals are complicated and have to be calculated numerically.

The way the integration is done for Normal distribution priors uses a numerical integration technique where the integral is reparameterized into a radial direction, and the number of parameters minus one angular directions. The radial part of the integral is handled using Radau-Gauss-Laguerre quadrature with an evaluation at radius=0. A randomized Mysovskikh quadrature is used to calculate the integral over the spherical part, which is equivalent to integrating over the surface of a hypersphere.

Note: If some of the prior distributions are not Normal, then the integral is reparameterized so that the new parameters have normal distribution, and then the radial-spherical integration method is applied. However, if the prior distribution set for the parameters does not lend itself to a solution, sometimes the process fails and gives the message that the Fisher information is singular in a region of the parameter space, and advises changing the prior distribution or the ranges of the parameters.

The following is a technical description for these two advanced options:

Number of Monte Carlo Samples

sets the number of octahedra per sphere. Because each octahedron is a fixed unit, this option can be thought of as setting the number of octahedra per sphere.

N Monte Carlo Spheres

are the number of nonzero radius values used. The default is two spheres and one center point. Each radial value requires integration over the angular dimensions. This is done by constructing a certain number of hyperoctahedra (the generalization of an octagon in arbitrary dimensions), and randomly rotating each of them.

Technical The reason for the approach given by these advanced options is to get good integral approximations much faster than using standard methods. For instance, with six parameters, using two radii and one sample per sphere, these methods give a generalized five- point rule that needs only 113 observations to get a good approximation. Using the most common approach (Simpson’s rule) would need 56 = 15,625 evaluations. The straight Monte Carlo approach also requires thousands of function evaluations to get the same level of quality in the answer. For more details, see Gotwalt, Jones, and Steinberg (2009).

Keep in mind that if the number of radii is set to zero, then just the center point is used, which gives a local design that is optimal for a particular value of the parameters. For some people this is good enough for their purposes. These designs are created much faster than if the integration is performed.