Power is calculated for the effects listed in the Model outline. These include continuous, discrete numeric, categorical, blocking, covariate, mixture, and covariate factors. The tests are for individual model parameters and for whole effects. For details on how power is calculated, see Power Calculations in Technical Details.
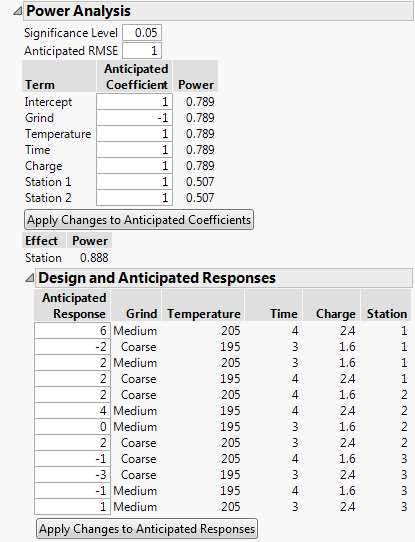
Power Analysis for Coffee Data.jmp shows the Power Analysis outline for the design in the Coffee Data.jmp sample data table, found in the Design Experiment folder. The model specified in the Model script is a main effects only model.
The top portion of the Power Analysis report opens with default values for the Anticipated Coefficients. See Power Analysis for Coffee Data.jmp. The default values are based on Delta. For details, see Advanced Options > Set Delta for Power.
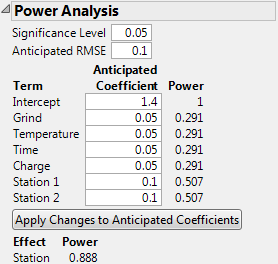
Possible Specification of Anticipated Coefficients for Coffee Data.jmp shows the top portion of the Power Analysis report where values have been specified for the Anticipated Coefficients. These values reflect the differences you want to detect.
A value for the coefficient associated with the model term. This value is used in the calculations for Power. These values are also used to calculate the Anticipated Response column in the Design and Anticipated Responses outline. When you set a new value in the Anticipated Coefficient column, click Apply Changes to Anticipated Coefficients to update the Power and Anticipated Response columns.
Note: The anticipated coefficients have default values of 1 for continuous effects. They have alternating values of 1 and –1 for categorical effects. You can specify a value for Delta be selecting Advanced Options > Set Delta for Power from the red triangle menu. If you change the value of Delta, the values of the anticipated coefficients are updated so that their absolute values are one-half of Delta. For details, see Advanced Options > Set Delta for Power.
Calculations use the specified Significance Level and Anticipated RMSE. For details of the power calculation, see Power for a Single Parameter in Technical Details.
When you set a new value in the Anticipated Coefficient column, click Apply Changes to Anticipated Coefficients to update the Power and Anticipated Response columns.
Calculations use the specified Significance Level and Anticipated RMSE. For details of the power calculation, see Power for a Categorical Effect in Technical Details.
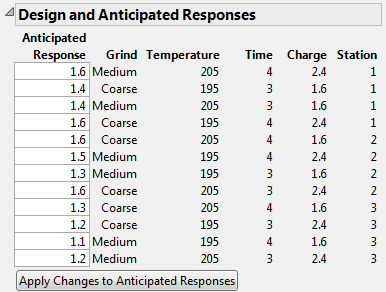
Anticipated Responses for Coffee Data.jmp shows the Design and Anticipated Responses outline corresponding to the specification of Anticipated Coefficients given in Possible Specification of Anticipated Coefficients for Coffee Data.jmp.
Click Apply Changes to Anticipate Responses to update both the Anticipated Coefficient and Power columns.
The response value obtained using the Anticipated Coefficient values as coefficients in the model. When the outline first appears, the calculation of Anticipated Response values is based on the default values in the Anticipated Coefficient column. When you set new values in the Anticipated Response column, click Apply Changes to Anticipated Responses to update the Anticipated Coefficient and Power columns.
When you set new values in the Anticipated Response column, click Apply Changes to Anticipated Responses to update the Anticipated Coefficient and Power columns.
Consider the design in the Coffee Data.jmp data table. Suppose that you are interested in the power of your design to detect effects of various magnitudes on Strength. Recall that Grind is a two-level categorical factor, Temperature, Time, and Charge are continuous factors, and Station is a three-level categorical (blocking) factor.
In this example, ignore the role of Station as a blocking factor. You are interested in the effect of Station on Strength. Since Station is a three-level categorical factor, it is represented by two terms in the Parameters list: Station 1 and Station 2.
Specifically, you are interested the probability of detecting the following changes in the mean Strength:
|
•
|
A change of 0.10 units as you vary Grind from Coarse to Medium.
|
|
•
|
A change of 0.10 units or more as you vary Temperature, Time, and Charge from their low to high levels.
|
You set 0.05 as your Significance Level. Your estimate of the standard deviation of Strength for fixed design settings is 0.1 and you enter this as the Anticipated RMSE.
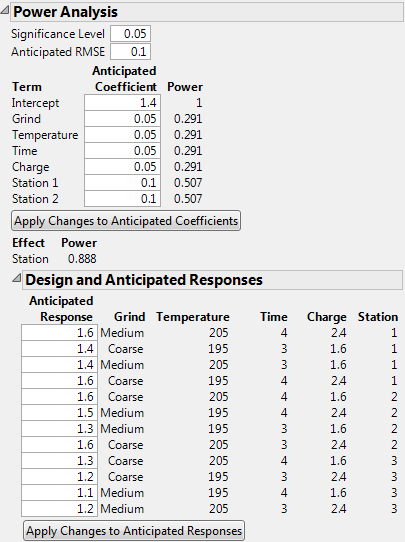
Power Analysis Outline with User Specifications in Anticipated Coefficients Panel shows the Power Analysis node with these values entered. Specifically, you specify the Significance Level, Anticipated RMSE, and the value of each Anticipated Coefficient.
Recall that Temperature is a continuous factor with coded levels of -1 and 1. Consider the test whose null hypothesis is that Temperature has no effect on Strength. Power Analysis Outline with User Specifications in Anticipated Coefficients Panel shows that the power of this test to detect a difference of 0.10 (=2*0.05) units across the levels of Temperature is only 0.291.
Now consider the test for the whole Station effect, where Station is a three-level categorical factor. Consider the test whose null hypothesis is that Station has no effect on Strength. This is the usual F test for a categorical factor provided in the Effect Tests report when you run Analyze > Fit Model. (See Effect Tests in the Fitting Linear Models book.)
The Power of this test is shown directly beneath the Apply Changes to Anticipated Coefficients button. The entries under Anticipated Coefficients for the model terms Station 1 and Station 2 are both 0.10. These settings imply that the effect of both stations is to increase Strength by 0.10 units above the overall anticipated mean. For these settings of the Station 1 and Station 2 coefficients, the effect of Station 3 on Strength is to decrease it by 0.20 units from the overall anticipated mean. Power Analysis Outline with User Specifications in Anticipated Coefficients Panel shows that the power of the test to detect a difference of at least this magnitude is 0.888.