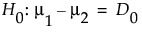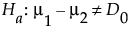The Sample Size and Power windows work similarly for one and two sample means; the Difference to Detect is the difference between two means. The comparison is between two random samples instead of one sample and a hypothesized mean.
where μ1 and μ2 are the two population means and D0 is the difference in the two means or the difference to detect. It is assumed that the populations of interest are normally distributed and the true difference is zero. Note that the power for this setting is the same as for the power when the null hypothesis is H0: μ1 − μ2 = 0 and the true difference is D0.
|
1.
|
Select DOE > Design Diagnostics > Sample Size and Power.
|
|
2.
|
Click the Two Sample Means button in the Sample Size and Power Window.
|
|
3.
|
Leave Alpha as 0.05.
|
|
4.
|
Enter 2 for Std Dev.
|
|
5.
|
Leave Extra Parameters as 0.
|
|
6.
|
Enter 1.5 as Difference to detect.
|
|
7.
|
Enter 30 for Sample Size.
|
|
8.
|
Leave Power blank.
|
|
9.
|
Click Continue.
|
The Power is calculated as 0.51. (See the left window in Plot of Power by Sample Size to Detect for a Given Difference.) This means that you have a 51% chance of detecting a significant difference between the two sample means when your significance level is 0.05, the difference to detect is 1.5, and each sample size is 15.
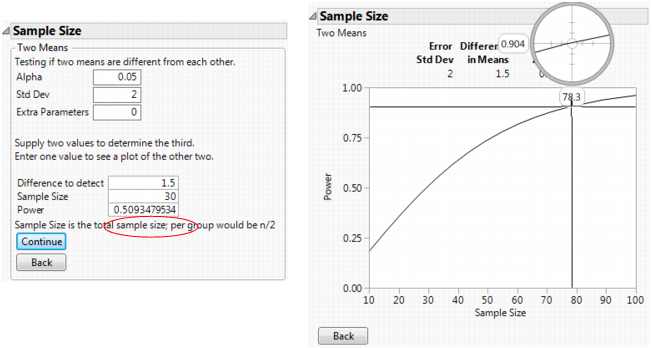
To have a greater power requires a larger sample. To find out how large, leave both Sample Size and Power blank for this same example and click Continue. Plot of Power by Sample Size to Detect for a Given Difference shows the resulting plot, with the crosshair tool estimating that a sample size of about 78 is needed to obtain a power of 0.9.