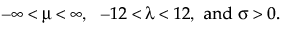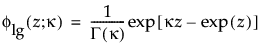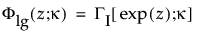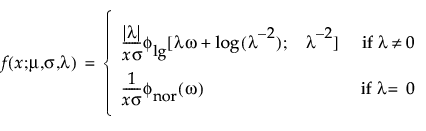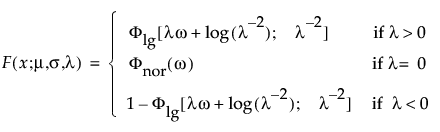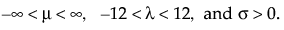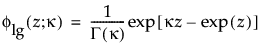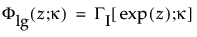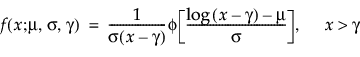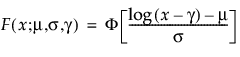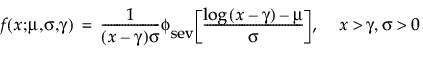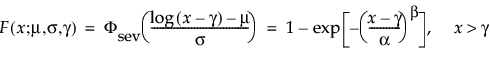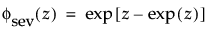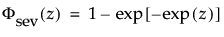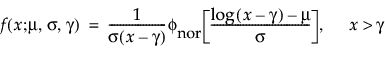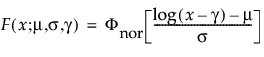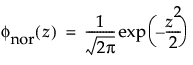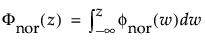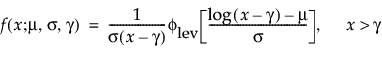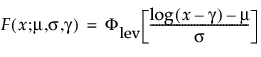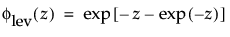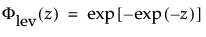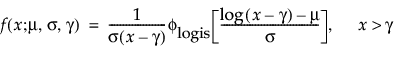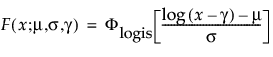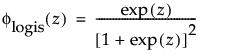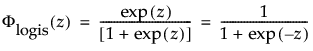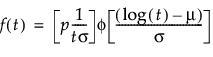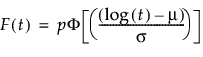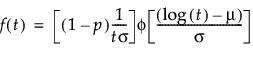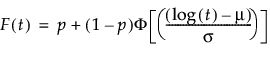This section provides details for the distributional fits in the Life Distribution platform. Meeker and Escobar (1998, ch. 2-5) is an excellent source of theory, application, and discussion for both the nonparametric and parametric details that follow.
The parameters of all distributions, unless otherwise noted, are estimated using maximum likelihood estimates (MLEs). The only exceptions are the threshold distributions. If the smallest observation is an exact failure, then this observation is treated as interval-censored with a small interval. The parameter estimates are the MLEs estimated from this slightly modified data set. Without this modification, the likelihood can be unbounded, so an MLE might not exist. This approach is similar to that described in Meeker and Escobar (1998, p. 275), except that only the smallest exact failure is censored. This is the minimal change to the data that guarantees boundedness of the likelihood function.
The Life Distribution platform offers two methods for calculating confidence intervals for the distribution parameters. These methods are labeled as Wald or Likelihood and can be selected in the launch window for the Life Distribution platform. Wald confidence intervals are used as the default setting. The computations for the confidence intervals for the cumulative distribution function (cdf) start with Wald confidence intervals on the standardized variable. Next, the intervals are transformed to the cdf scale (Nelson 1982, pp. 332–333 and pp. 346-347). The confidence intervals given in the other graphs and profilers are transformed Wald intervals (Meeker and Escobar 1998, ch. 7). Joint confidence intervals for the parameters of a two-parameter distribution are shown in the log-likelihood contour plots. They are based on approximate likelihood ratios for the parameters (Meeker and Escobar 1998, ch. 8).
Note: Many distributions in the Life Distribution platform are parameterized by location and scale. For lognormal fits, the median is also provided. A threshold parameter is also included in threshold distributions. Location corresponds to μ, scale corresponds to σ, and threshold corresponds to γ.
The Weibull distribution can be used to model failure time data with either an increasing or a decreasing hazard rate. It is used frequently in reliability analysis because of its tremendous flexibility in modeling many different types of data, based on the values of the shape parameter, β. This distribution has been successfully used for describing the failure of electronic components, roller bearings, capacitors, and ceramics. Various shapes of the Weibull distribution can be revealed by changing the scale parameter, α, and the shape parameter, β. The Weibull pdf and cdf are commonly represented as follows:
where α is a scale parameter, and β is a shape parameter. The Weibull distribution is particularly versatile because it reduces to an exponential distribution when β = 1. An alternative parameterization commonly used in the literature and in JMP is to use σ as the scale parameter and μ as the location parameter. These are easily converted to an α and β parameterization using the following definitions:
The pdf and the cdf of the Weibull distribution are also expressed as a log-transformed smallest extreme value distribution (SEV). This uses a location scale parameterization, with μ = log(α) and σ = 1/β,
are the pdf and cdf, respectively, for the standardized smallest extreme value (μ = 0, σ = 1) distribution.
are the pdf and cdf, respectively, for the standardized logistic or logis distribution(μ = 0, σ = 1).
are the pdf and cdf, respectively, for the standardized largest extreme value LEV(μ = 0, σ = 1) distribution.
The normal distribution is the most widely used distribution in most areas of statistics because of its relative simplicity and the ease of applying the central limit theorem. However, it is rarely used in reliability. It is most useful for data where μ > 0 and the coefficient of variation (σ / μ) is small. Because the hazard function increases with no upper bound, it is particularly useful for data exhibiting wear-out failure. Examples include incandescent light bulbs, toaster heating elements, and mechanical strength of wires. The pdf and cdf are:
This non-symmetric (left-skewed) distribution is useful in two cases. The first case is when the data indicate a small number of weak units in the lower tail of the distribution (the data indicate the smallest number of many observations). The second case is when σ is small relative to μ, because probabilities of being less than zero, when using the SEV distribution, are small. The smallest extreme value distribution is useful to describe data whose hazard rate becomes larger as the unit becomes older. Examples include human mortality of the aged and rainfall amounts during a drought. This distribution is sometimes referred to as a Gumbel distribution. The pdf and cdf are:
are the pdf and cdf, respectively, for the standardized smallest extreme value, SEV(μ = 0, σ = 1) distribution.
are the pdf and cdf, respectively, for the standardized logistic or logis distribution (μ = 0, σ = 1).
This right-skewed distribution can be used to model failure times if σ is small relative to μ > 0. This distribution is not commonly used in reliability but is useful for estimating natural extreme phenomena, such as a catastrophic flood heights or extreme wind velocities. The pdf and cdf are:
are the pdf and cdf, respectively, for the standardized largest extreme value LEV(μ = 0, σ = 1) distribution.
where θ is a scale parameter and γ is both the threshold and the location parameter. Reliability analysis frequently uses the one-parameter exponential distribution, with γ = 0. The exponential distribution is useful for describing failure times of components exhibiting wear-out far beyond their expected lifetimes. This distribution has a constant failure rate, which means that for small time increments, failure of a unit is independent of the unit’s age. The exponential distribution should not be used for describing the life of mechanical components that can be exposed to fatigue, corrosion, or short-term wear. This distribution is, however, appropriate for modeling certain types of robust electronic components. It has been used successfully to describe the life of insulating oils and dielectric fluids (Nelson 1990, p. 53).
are the pdf and cdf, respectively, for the log-gamma variable and κ > 0 is a shape parameter. The standardized distributions above are dependent upon the shape parameter κ.
Note: In JMP, the shape parameter, λ, for the generalized gamma distribution is bounded between [-12,12] to provide numerical stability.
are the pdf and cdf, respectively, for the standardized log-gamma variable and κ > 0 is a shape parameter.
The standardized distributions above are dependent upon the shape parameter κ. Meeker and Escobar (1998, ch. 5) give a detailed explanation of the extended generalized gamma distribution.
Note: In JMP, the shape parameter, λ, for the generalized gamma distribution is bounded between [-12,12] to provide numerical stability.
Threshold Distributions are log-location-scale distributions with threshold parameters. Some of the distributions above are generalized by adding a threshold parameter, denoted by γ. The addition of this threshold parameter shifts the left endpoint of the distribution away from 0. Threshold parameters are sometimes called shift, minimum, or guarantee parameters because all units survive at least until threshold time. Note that while adding a threshold parameter shifts the distribution on the time axis, the shape, and spread of the distribution are not affected. Threshold distributions are useful for fitting moderately to heavily shifted distributions. The general forms for the pdf and cdf of a log-location-scale threshold distribution are:
where φ and Φ are the pdf and cdf, respectively, for the specific distribution. Examples of specific threshold distributions are shown below for the Weibull, lognormal, Fréchet, and loglogistic distributions, where, respectively, the SEV, Normal, LEV, and logis pdfs and cdfs are appropriately substituted.
are the pdf and cdf, respectively, for the standardized smallest extreme value, SEV(μ = 0, σ = 1) distribution.
are the pdf and cdf, respectively, for the standardized largest extreme value LEV(μ = 0, σ = 1) distribution.
are the pdf and cdf, respectively, for the standardized logistic or logis distribution (μ = 0, σ = 1).
p is the defective subpopulation fraction
t is the time of measurement for the lifetime event
μ and σ are estimated by calculating the usual maximum likelihood estimations after removing zero values from the original data
φ(z) and Φ(z) are the density and cumulative distribution function, respectively, for a standard distribution. For example, for a Weibull distribution,
See Tobias and Trindad (2012, p. 321) for more information about defective subpopulation models.
The defective subpopulation model is also known as a limited failure population model in Meeker and Escobar (1998, ch. 11).
Zero-inflated distributions are used when some proportion (p) of the data fail at t = 0. When the data contain more zeros than expected by a standard model, the number of zeros is inflated. When the time-to-event data contain zero as the minimum value in the Life Distribution platform, four zero-inflated distributions are available. These distributions include:
p is the proportion of zero data values,
t is the time of measurement for the lifetime event,
μ and σ are estimated by calculating the usual maximum likelihood estimations after removing zero values from the original data,
φ(z) and Φ(z) are the density and cumulative distribution function, respectively, for a standard distribution. For example, for a Weibull distribution,
See Lawless (2003, p. 34) for more information about zero-inflated distributions. Substitute p = 1 - p and S1(t) = 1 - Φ(t) to obtain the form shown above.
See Tobias and Trindade (1995, p. 232) for more information about reliability distributions. This reference gives the general form for mixture distributions. Using the parameterization in Tobias and Trindade, the form above can be found by substituting α = p, Fd(t) = 1, and FN(t) = Φ(t).
|
•
|
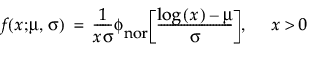
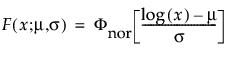
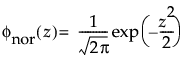
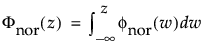
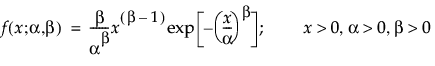
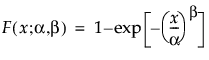
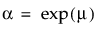
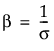
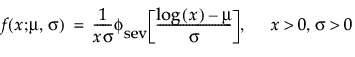
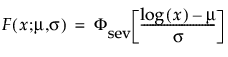
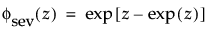
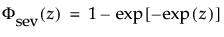
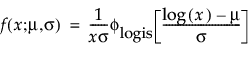
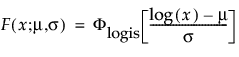
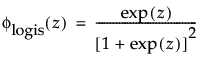
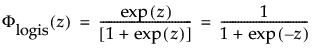
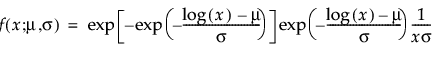
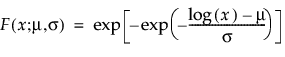
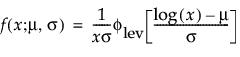
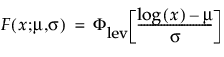
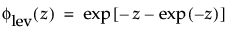
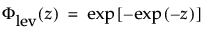
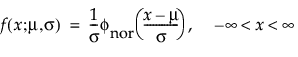
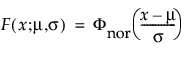
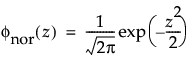
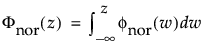
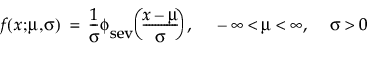
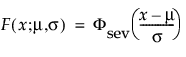
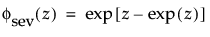
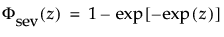
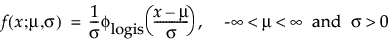
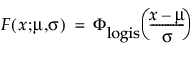
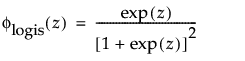
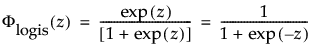
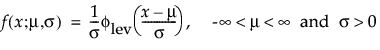
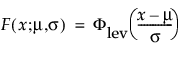
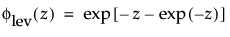
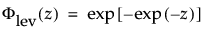
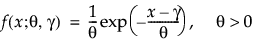
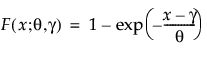
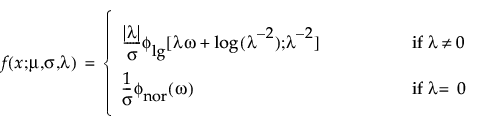
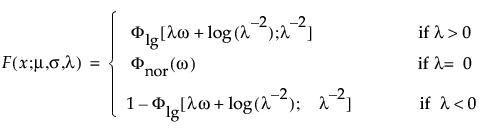
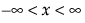 ,
,