Contributions
When computing contribution proportions, JMP zeros out negative contributions.
PCA and PLS T2 Contributions
The T2 contributions for a PCA or PLS model with p variables and k components are calculated as:
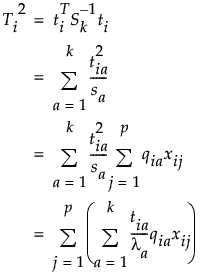
where
ti = the vector of k scores for the ith observation
Sk = the diagonal sample covariance matrix of the k scores for historical observations. For PCA models,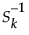 
is the diagonal eigenvalue matrix.
sa is the ath component of Sk
rja is the jth component of the ath eigenvector for PCA models and the ath column of the Rk matrix for PLS models. Rk is the matrix used to relate the score matrix, Tk to the X matrix, such that Tk=XRk.
xij is the value of the jth variable for the ith observation.
Note that since
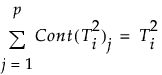
the contribution proportion of variable j is defined as:
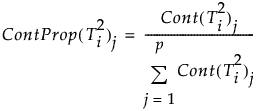
For more information about PCA contributions, see Kourti and MacGregor (1996). For more information about PLS contributions, see Li et al. (2009).
DModX
For PCA and PLS models, the contribution of variable j to DModXi is defined as:
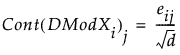
Note that since
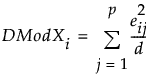
the contribution proportion of variable j is defined as:
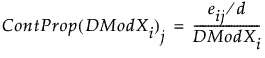
SPE Contributions
For PCA and PLS models, the contribution of variable j to SPEi is defined as:
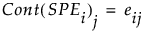
Note that since
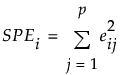
the contribution proportion of variable j is defined as:
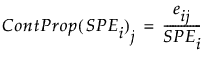
Score Contributions
The score contribution computation is the same as T2 contributions with the following exceptions:
• for PCA models only the columns corresponding to the score dimensions are used from the Qk matrix
• for PLS models only the columns corresponding to the score dimensions are used from the Rk matrix.