Uniform Designs
The Uniform design minimizes the discrepancy between the design points (empirical uniform distribution) and a theoretical uniform distribution.
Note: These designs are most useful for getting a simple and precise estimate of the integral of an unknown function. The estimate is the average of the observed responses from the experiment.
1. Select DOE > Special Purpose > Space Filling Design.
2. Enter responses, if necessary, and factors.
See Responses.
3. Alter the factor level values to 0 and 1.
4. Click Continue.
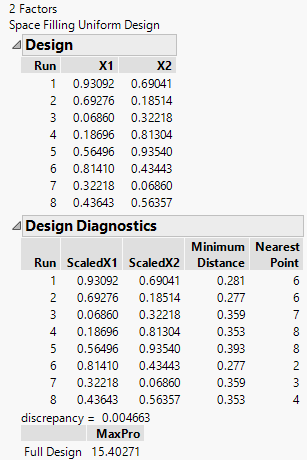
5. In the design specification dialog, specify a sample size. This example uses a sample size of eight (Number of Runs).
6. Click the Uniform button. JMP creates this design and displays the design runs and the design diagnostics as shown in Figure 21.14.
Note: The emphasis of the Uniform design method is not to spread out the points. The minimum distances in Figure 21.14 vary substantially.
Figure 21.14 Factor Settings and Diagnostics for Uniform Space-Filling Designs with Eight Runs
7. Click Make Table.
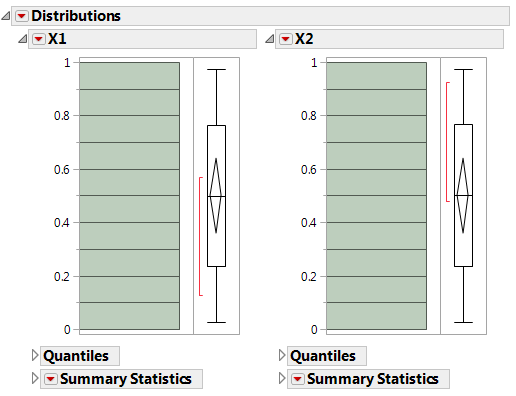
A Uniform design does not guarantee even spacing of the factor levels. However, increasing the number of runs and running a distribution on each factor (use Analyze > Distribution) shows flat histograms.
Figure 21.15 Histograms Are Flat for Each Factor When Number of Runs Is Increased to 20