Example of K Means Cluster
In this example, you use the Cytometry.jmp sample data table to cluster observations using K Means Cluster. Cytometry is used to detect markers of the surface of cells and the readings from these markers help diagnose certain diseases. In this example, the observations are grouped based on readings of four markers in a cytometry analysis.
1. Select Help > Sample Data Library and open Cytometry.jmp
2. Select Analyze > Clustering > K Means Cluster.
3. Select CD3, CD8, CD4, and MCB and click Y, Columns.
4. Click OK.
5. Enter 3 next to Number of Clusters.
6. Enter 15 next to Range of Clusters (Optional).
Because the Range of Clusters is set to 15, the platform provides fits for 3 to 15 clusters. You can then determine your preferred number of clusters.
7. Click Go.
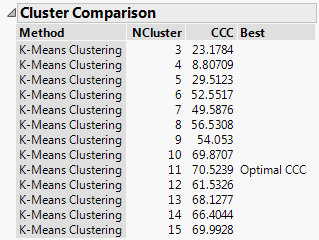
Figure 13.2 Cluster Comparison Report
The Cluster Comparison report appears at the top of the report window. The best fit is determined by the highest CCC value. In this case, the best fit occurs when you fit 11 clusters.
8. Scroll to the K Means NCluster=11 report.
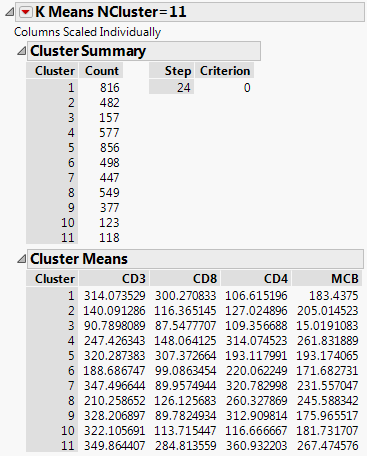
Figure 13.3 K Means NCluster=11 Report
The Cluster Summary report shows the number of observations in each of the eleven clusters. The Cluster Means report shows the means of the four marker readings for each cluster.
9. Click the K Means NCluster=11 red triangle and select Parallel Coord Plots.
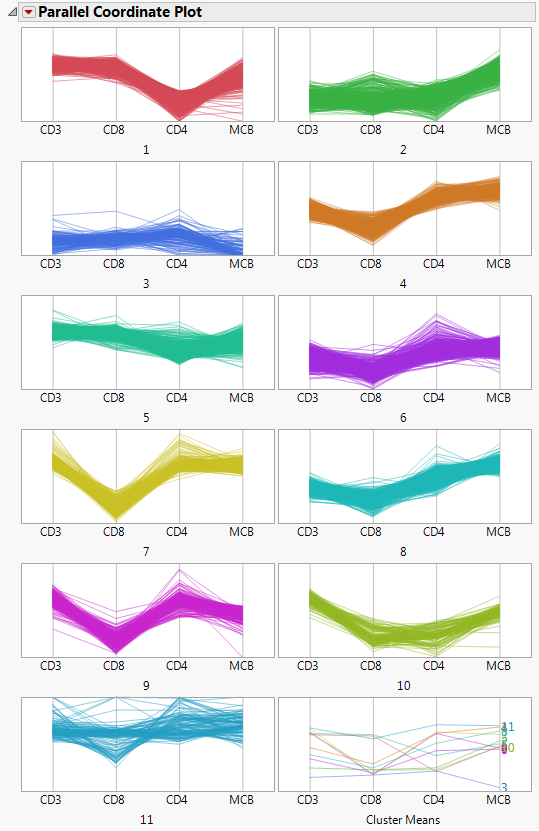
Figure 13.4 Parallel Coordinate Plots for Cytometry Data
The Parallel Coordinate Plots display the structure of the observations in each cluster. Use these plots to see how the clusters differ. Clusters 4, 6, 7, 8, and 9 tend to have comparatively low CD8 values and high CD4 values. Cluster 1, on the other hand, has higher CD8 values and lower CD4 values.
10. Click the K Means NCluster=11 red triangle and select Biplot.
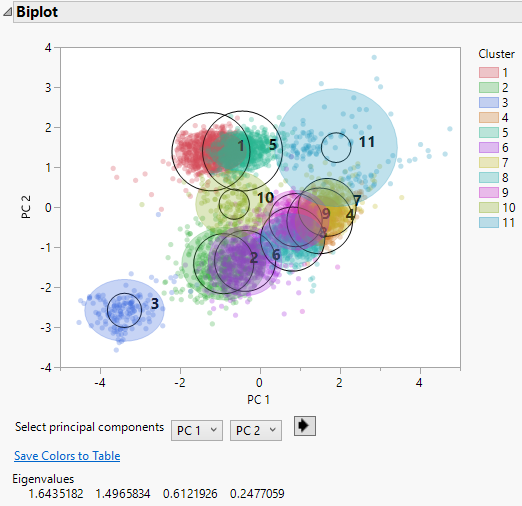
Figure 13.5 Biplot for Cytometry Data
A legend that identifies the colors of the clusters is shown to the right of the plot. The clusters that appear to be most separated from the others based on their first two principal components are clusters 3, 10, and 11. This is supported by their parallel coordinate plots in Figure 13.4, which differ from the plots for the other clusters. Use the list below the plot to see the biplot for other combinations of principal components.