Functional Model Fits

All of the model fits in the Functional Data Explorer platform rely on basis function expansion. Basis functions are a set of independent functions. Any function, f(t), can be approximated by taking a linear combination of K basis functions, denoted as φk. In general, a function is approximated as follows:

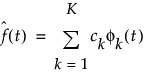
where the ck parameters are the basis coefficients. The amount of smoothing is determined by the number of basis functions, K. For more information about basis function expansion, see Ramsay and Silverman (2005).

The k = 1,..., K functions that define the Fourier basis are defined such that φ0 = 1, φ2k-1 = sin(rωt), and φ2k = cos(rωt). Then, the approximated function is as follows:

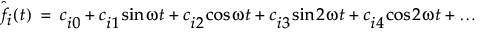
This approximates a periodic function with period A defined as A = 2π/ω. The coefficients are a combination of fixed basis function coefficients and random coefficients by function. Each c is defined as follows:

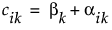
where βk is the fixed coefficient for basis function k and αik is the random coefficient for basis function k for a specific functional process i. For the Fourier Basis model, the estimates for the βk and αik parameters are found in the Basis Function Coefficients table and Random Coefficients by Function table, respectively.

Fourier basis models have an intercept term and an equal number of sine and cosine terms, which are referred to as Fourier pairs. Therefore, K is always odd. For example, if K = 7, there is an intercept term and three Fourier pairs.