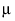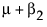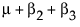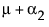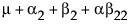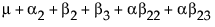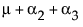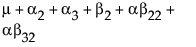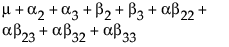Ordinal Factors
Factors marked with the ordinal modeling type are coded differently than nominal factors. The parameter estimates are interpreted differently, the tests are different, and the least squares means are different.
For ordinal factors, the first level of the factor is a control or baseline level, and the parameters measure the effect on the response as the ordinal factor is set to each succeeding level. The ordinal factor coding is appropriate for factors that contain levels that represent various doses, where the first dose is zero. The following table shows an example of a three-level ordinal factor:
|
Term |
Coded Column |
|
|
|
A |
a2 |
a3 |
|
|
A1 |
0 |
0 |
control level, zero dose |
|
A2 |
1 |
0 |
low dose |
|
A3 |
1 |
1 |
higher dose |
The pattern for the design is such that the lower triangle is ones with zeros elsewhere.
For a simple main-effects model, this can be written as follows:
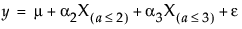
noting that μ is the expected response at A = 1, μ + α2 is the expected response at A = 2, and μ + α2 + α3 is the expected response at A = 3. Thus, α2 estimates the effect moving from A = 1 to A = 2 and α3 estimates the effect moving from A = 2 to A = 3.
If all the parameters for an ordinal main effect have the same sign, then the response effect is monotonic across the ordinal levels.
Ordinal Interactions
The ordinal interactions, as with nominal effects, are produced with a horizontal direct product of the columns of the factors. Consider an example with two ordinal factors A and B, where each factor has three levels. The ordinal coding in JMP produces the design matrix shown next. The pattern for the interaction is a block lower-triangular matrix of lower-triangular matrices of ones.
|
|
|
|
|
| A*B | |||
|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
| A2 | A3 | ||
A | B | A2 | A3 | B2 | B3 | B2 | B3 | B2 | B3 |
A1 | B1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
A1 | B2 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
A1 | B3 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
A2 | B1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
A2 | B2 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
A2 | B3 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
A3 | B1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
A3 | B2 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
A3 | B3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Note: When you test to see whether there is no effect, there is not much difference between nominal and ordinal factors for simple models. However, there are major differences when interactions are specified. We recommend that you use nominal rather than ordinal factors for most models.
Hypothesis Tests for Ordinal Crossed Models
To see what the parameters mean, examine this table of the expected cell means in terms of the parameters, where μ is the intercept, α2 is the parameter for level A2, and so on.
| B1 | B2 | B3 |
A1 |
|
|
|
A2 |
|
|
|
A3 |
|
|
|
Note that the main effect test for A is really testing the A levels holding B at the first level. Similarly, the main effect test for B is testing across the top row for the various levels of B holding A at the first level. This is the appropriate test for an experiment where the two factors are both doses of different treatments. The main question is the efficacy of each treatment by itself, and fewer points are devoted to looking for drug interactions when doses of both drugs are applied. In some cases, it might even be dangerous to apply large doses of each drug.
Note that each cell’s expectation can be obtained by adding all the parameters associated with each cell that is to the left and above it, inclusive of the current row and column. The expected value for the last cell is the sum of all the parameters.
Though the hypothesis tests for effects contained by other effects differs with ordinal and nominal codings, the test of effects not contained by other effects is the same. In the crossed design above, the test for the interaction would be the same no matter whether A and B were fit nominally or ordinally.
Ordinal Least Squares Means
As stated previously, least squares means are the predicted values corresponding to some combination of levels, after setting all the other factors to some neutral value. JMP defines the neutral value for an effect with uninvolved ordinal factors as the effect at the first level, meaning the control, or baseline level.
This definition of least squares means for ordinal factors maintains the idea that the hypothesis tests for contained effects are equivalent to tests that the least squares means are equal.
Singularities and Missing Cells in Ordinal Effects
With the ordinal coding, you are saying that the first level of the ordinal effect is the baseline. It is thus possible to get good tests on the main effects even when there are missing cells in the interactions—even if you have no data for the interaction.
Example with Missing Cell
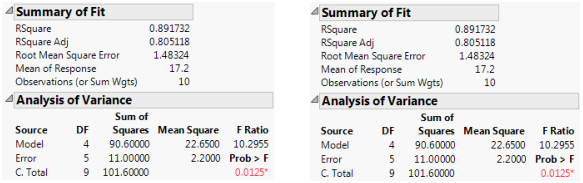
The example is the same as above, with two observations per cell except that the A3B2 cell has no data. You can now compare the results when the factors are coded nominally with results when they are coded ordinally. The model fit is the same, as seen in Figure A.2.
Y | A | B |
12 | 1 | 1 |
14 | 1 | 1 |
15 | 1 | 2 |
16 | 1 | 2 |
17 | 2 | 1 |
17 | 2 | 1 |
18 | 2 | 2 |
19 | 2 | 2 |
20 | 3 | 1 |
24 | 3 | 1 |
Figure A.2 Summary Information for Nominal Fits (Left) and Ordinal Fits (Right)
The parameter estimates are very different because of the different coding. Note that the missing cell affects estimability for some nominal parameters but for none of the ordinal parameters.
Figure A.3 Parameter Estimates for Nominal Fits (Left) and Ordinal Fits (Right)
The singularity details show the linear dependencies (and also identify the missing cell by examining the values).
Figure A.4 Singularity Details for Nominal Fits (Left) and Ordinal Fits (Right)
The effect tests lose degrees of freedom for nominal. In the case of B, there is no test. For ordinal, there is no loss because there is no missing cell for the base first level.
Figure A.5 Effects Tests for Nominal Fits (Left) and Ordinal Fits (Right)
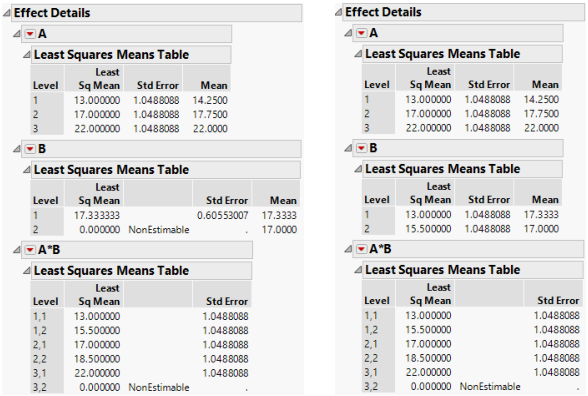
The least squares means are also different. The nominal LSMs are not all estimable, but the ordinal LSMs are. You can verify the values by looking at the cell means. Note that the A*B LSMs are the same for the two. Figure A.6 shows least squares means for nominal and ordinal fits.
Figure A.6 Least Squares Means for Nominal Fits (Left) and Ordinal Fits (Right)