Poisson Generalized Regression Example
The Liver Cancer.jmp sample data table contains liver cancer Node Count values for 136 patients. It also includes measurements on six potentially related variables: BMI, Age, Time, Markers, Hepatitis, and Jaundice. These variables are described in the Notes column property in each column of the data table. To view the Notes column property, right-click a column name, select Column Info, and select Notes under Column Properties.
This example develops a prediction model for Node Count using the six predictors. Node Count is modeled using a Poisson distribution.
1. Select Help > Sample Data Library and open Liver Cancer.jmp.
2. Select Analyze > Fit Model.
3. Select Node Count from the Select Columns list and click Y.
4. Select BMI through Jaundice and click Macros > Factorial to Degree.
This adds all terms up to degree 2 (the default in the Degree box) to the model.
5. Select Validation from the Select Columns list and click Validation.
6. From the Personality list, select Generalized Regression.
7. From the Distribution list, select Poisson.
8. Click Run.
The Generalized Regression report that appears contains a Model Comparison report, a Model Launch control panel, and a Poisson Maximum Likelihood with Validation Column report. Note that the default estimation method is the Lasso.
9. Select the Adaptive box.
10. Click Go.
11. Click the red triangle next to Poisson Adaptive Lasso with Validation Column and select Select Nonzero Terms.
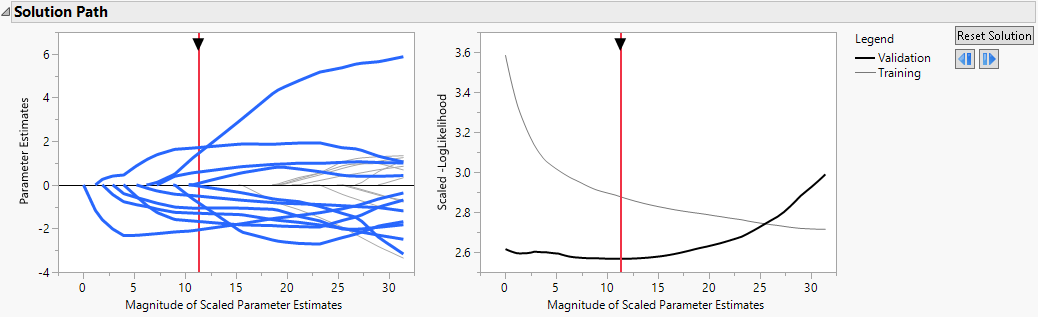
The Solution Path is shown in Figure 7.1. The paths for terms that have nonzero coefficients are highlighted. Think of the solution paths as moving from right to left across the plot, as the solutions shrink farther from the MLE. A number of terms have paths that shrink them to zero fairly early.
The vertical axis in the Solution Path Plot represents the values of the parameter estimates for the standardized predictors. The vertical red line indicates their values at the optimal shrinkage, as determined by cross validation. At this point, 11 terms have nonzero coefficients. Notice that the vertical red line indicates the minimum Scaled −LogLikelihood value in the Validation set.
Figure 7.1 Solution Path for Adaptive Lasso Fit with Nonzero Terms Highlighted
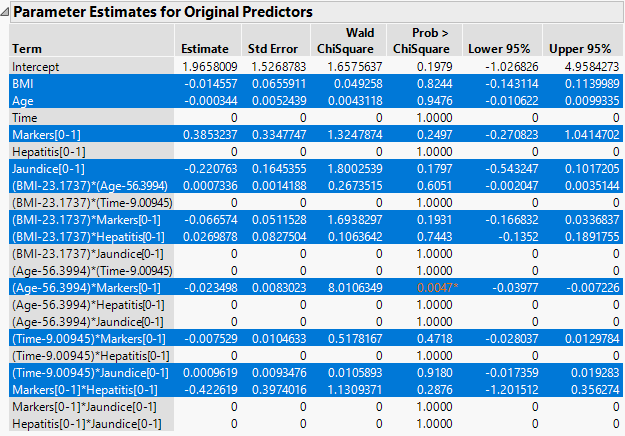
The Parameter Estimates for Original Predictors report (Figure 7.2) shows the parameter estimates for the uncentered and unscaled data. The 11 terms with nonzero parameter estimates are highlighted. These include interaction effects. In the data table, all six predictor columns are selected because every predictor column appears in a term that has a nonzero coefficient.
In the Effect Tests report, the 10 effects with zero coefficient estimates are designated as Removed. The Effect Tests report indicates that only one effect is significant at the 0.05 level: the Age*Markers interaction.
12. Click the row for (Age - 56.3994)*Markers[0-1] in the Parameter Estimates for Original Predictors report.
This action highlights that effect’s path in the Solution Path Plot and selects the columns Age and Markers in the data table.
Figure 7.2 Parameter Estimates Report with Nonzero Terms Highlighted
13. Click the red triangle next to Poisson Adaptive Lasso with Validation Column and select Save Columns > Save Prediction Formula and Save Columns > Save Variance Formula.
Two columns are added to the data table: Node Count Prediction Formula and Node Count Variance.
14. In the data table, right-click either column heading and select Formula to view the formula. Alternatively, click the plus sign to the right of the column name in the Columns panel.
The prediction formula in the Save Prediction Formula column applies the exponential function to the estimated linear part of the model. The prediction variance formula in Node Count Variance is given by the identical formula, because the variance of a Poisson distribution is equal to its mean.