Comparison of a D-Optimal and an I-Optimal Response Surface Design
In this example, you explore the differences between I-optimality and D-optimality in the context of a two-factor response surface design.
I-Optimal Design
1. Select DOE > Custom Design.
2. Type 2 next to Add N Factors.
3. Click Add Factor > Continuous.
4. Click Continue.
5. Click RSM.
Quadratic and interactions terms for X1 and X2 are added to the model. Because you added RSM terms, the Recommended optimality criterion changes from D-Optimal to I-Optimal. You can see this later in the Design Diagnostics outline.
Note: Setting the Random Seed in step 6 and Number of Starts in step 7 reproduces the exact results shown in this example. In constructing a design on your own, these steps are not necessary.
6. (Optional) Click the Custom Design red triangle, select Set Random Seed, type 383570403, and click OK.
7. (Optional) Click the Custom Design red triangle, select Number of Starts, type 8, and click OK.
8. Click Make Design.
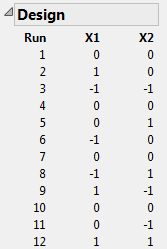
Figure 5.40 I-Optimal Design
In this I-optimal design, runs 1, 4, 7, and 10 are at the center point (X1 = 0 and X2 = 0). I-optimal designs tend to place more runs in the center (and consequently fewer runs at the extremes) of the design space than do D-optimal designs. You can compare this design to the D-optimal design shown in Figure 5.42.
9. Open the Design Evaluation > Prediction Variance Profile outline.
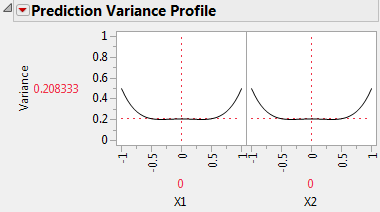
Figure 5.41 Prediction Variance Profile for I-Optimal Model
The relative prediction variance of the expected response is smallest in the center of the design space.
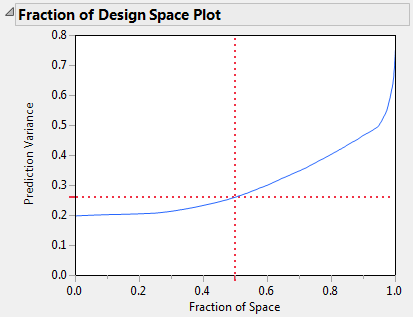
10. Open the Fraction of Design Space Plot outline.
The Fraction of Design Space Plot appears on the left in Figure 5.44. When the Fraction of Space is 0.95, the vertical coordinate of the blue curve is about 0.5. This means that for about 95% of the design space, the relative prediction variance is below 50% of the error variance.
This Custom Design window contains your I-optimal design. Keep this window open. In the next section, you generate a D-optimal design, and compare the two.
D-Optimal Design
To compare Prediction Variance Profile and Fraction of Design Space plots for the I- and D-optimal designs:
1. In the Custom Design window containing your I-optimal design, click the Custom Design red triangle and select Save Script to Script Window.
A window appears, showing a script that reproduces your work.
2. In this new script window, select Edit > Run Script.
A duplicate Custom Design window appears, but with the Design Evaluation outlines closed.
3. In this new Custom Design window, click Back.
4. Click the Custom Design red triangle and select Optimality Criterion > Make D-Optimal Design.
5. (Optional) Click the Custom Design red triangle, select Set Random Seed, type 383570403, and click OK.
6. Click Make Design.
You current Custom Design window contains your D-optimal design.
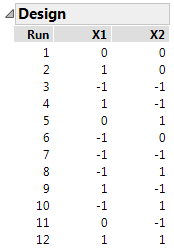
Figure 5.42 D-Optimal Design
In this D-optimal design, run 1 is the only run at the center point. D-optimal designs tend to place more runs at the extremes of the design space than do I-optimal designs. Recall that the I-optimal design had four center runs (Figure 5.40).
7. Open the Design Evaluation > Prediction Variance Profile outline.
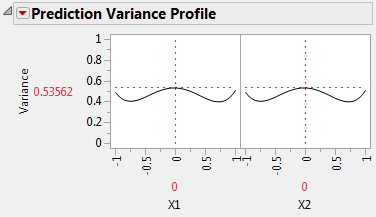
Figure 5.43 Prediction Variance Profile for D-Optimal Model
At the center of the design region, the relative prediction variance is 0.53562, as compared to 0.208333 for the I-optimal design (Figure 5.41). This means that the relative standard error is 0.732 for the D-optimal design and 0.456 for the I-optimal design. All else being equal, at the center of the design region, confidence intervals for the expected response based on the D-optimal design are about 60% wider than those based on the I-optimal design.
The Design outline shows that the D-optimal design has nine design points, one for every combination of X1 and X2 set to -1, 0, 1. The D-optimality criterion attempts to keep the relative prediction variance low at each of these design points. Explore the variance at the extremes of the design region by moving the sliders for X1 and X2 to -1 and 1. Note that the variance at these extreme points is usually smaller than the variance for the I-optimal design at these points.
8. Open the Design Evaluation > Fraction of Design Space Plot outline.
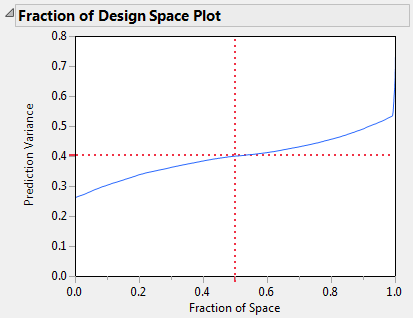
The Fraction of Design Space Plot appears on the right in Figure 5.44.
Figure 5.44 Fraction of Design Space Plots (I-Optimal on left, D-Optimal on right)
The red cross-hairs in each plot indicate the maximum prediction variance for 50% of the design space. For 50% of the design space, the prediction variance for the I-optimal design falls below about 0.27. For the D-optimal design, the prediction variance is about 0.4.
9. Right-click in the Fraction of Design Space Plot for your I-optimal design. Select Edit > Copy Frame Contents.
10. Right-click in the Fraction of Design Space Plot for your D-optimal design. Select Edit > Paste Frame Contents.
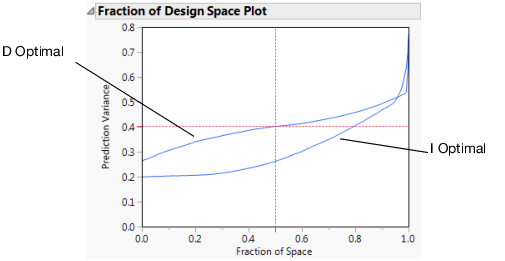
Figure 5.45 Fraction of Design Space Plots Superimposed
The variance curve for the I-optimal design is below the curve for the D-optimal design over at least 90% of the design space. This reflects the fact that I-optimality attempts to minimize prediction variance over all of the design space. In contrast, D-optimality focuses on reducing prediction variance at the design points.