Construct Model Effects
This section describes the options that you can use to facilitate entering effects into your model. Examples of how these options can be used to obtain specific types of models are given in Examples of Model Specifications and Their Model Fits.
Add
Adds effects to the model. These effects can either be added directly from the Select Columns list or they can be selected in that list and modified using Macros or Attributes. Effects can also be created and added, or modified, using Cross and Nest. The modeling types of the variables involved in the effect, as well as any Attribute assigned to the effect, determine how that effect is treated in the model.
Note: To remove an effect from the Construct Model Effects list, double-click the effect, or select it and click Remove or press Backspace or Delete.
Cross
Creates interaction or polynomial effects. Select two or more variables in the Select Columns list and click Cross. Or, select one or more variables in the Select Columns list and one or more effects in the Construct Model Effects list and click Cross.
See Statistical Details, for a discussion of how crossed effects are parameterized and coded.
Note: You can construct effects that combine up to ten columns as crossed and nested.
Example of Crossed Effects
Suppose that a product coating requires a dye to be applied. Both Dye pH and Dye Concentration are suspected to have an effect on the coating color. To understand their effects, you design an experiment where Dye pH and Dye Concentration are each set at a high and low level. It is possible that the effect of Dye pH on the color is more pronounced at the high level of Dye Concentration than at its low level. This is known as an interaction. To model this possible interaction, you include the crossed term, Dye pH * Dye Concentration, in the Construct Model Effects list. This enables JMP to test for an interaction.
Nest
Creates nested effects. If the levels of one effect (B) occur only within a single level of another effect (A), then B is said to be nested within A. The notation B[A], which is read as “B nested within A,” is typically used. Note that nesting defines a hierarchical relationship. A is called the outside effect and B is called the inside effect. Nested terms must be categorical.
Note: The nesting terms must be specified in order from outer to inner. For example, if B is nested within A, and C is nested within B, then the model is specified as A, B[A], C[B,A] (or, equivalently, A, B[A], C[A,B]). You can construct effects that combine up to ten columns as crossed and nested.
Example of Nested Effects
As an illustration of nesting, consider the math teachers in each of two schools. One school has three math teachers; the other school has two math teachers. Each teacher in each school teaches two or three classes consisting of non-overlapping groups of students. In this example, classes (C) are nested within teachers (B), and teachers (B) are nested within schools (A). Enter these effects in the Fit Model launch window:
1. Add both A and B to the Construct Model Effects panel.
2. In the Construct Model Effects panel, select B.
3. In the Select Columns list, select A.
4. Click Nest. This converts B to the effect B[A].
5. Add C to the Construct Model Effects panel.
6. In the Construct Model Effects panel, select C.
7. In the Select Columns list, select A and B.
8. Click Nest. The converts C to the effect C[A, B].
Macros
In the Macros list, select options to automatically generate the effects for commonly used models and enter them into the Construct Model Effects list:
Full Factorial
Creates all main effects and interactions for the columns selected in the Select Columns list. These are entered in an order that is based on the order in which the main effects are listed in the Select Columns list. For an alternate ordering, see Factorial Sorted, in this table.
Factorial to Degree
Creates all main effects, but only interactions up to a specified degree (order). Specify the degree in the Degree box beneath the Macros button.
Factorial Sorted
Creates the same set of effects as the Full Factorial option but lists them in order of degree. All main effects are listed first, followed by all two-way interactions, then all three-way interactions, and so on.
Response Surface
Creates main effects, two-way interactions, and quadratic terms. The selected main effects are given the response surface attribute, denoted RS. When the RS attribute is applied to main effects and the Standard Least Squares personality is selected, a Response Surface report is provided. This report gives information about critical values and the shape of the response surface.
See also Response Surface Effect in Attributes and Response Surface Designs in the Design of Experiments Guide.
Mixture Response Surface
Creates main effects and two-way interactions. Main effects have the response surface (RS) and mixture (Mixture) attributes. In the Standard Least Squares personality, the Mixture attribute causes a mixture model to be fit. The RS attribute creates a Response Surface report that is specific to mixture models.
See also Mixture Effect in Attributes and Response Surface Designs in the Design of Experiments Guide.
Polynomial to Degree
Creates main effects and polynomial terms up to a specified degree. Specify the degree in the Degree box beneath the Macros button.
Scheffé Cubic
Creates main effects, interactions, and Scheffé cubic terms, which are useful in specifying response surfaces for mixture experiments. This macro creates a complete cubic model.
When you fit a third-degree polynomial model to a mixture, you must not introduce even-powered terms, for example, X1*X1*X2, because they are not estimable. However, it turns out that a complete polynomial specification of the surface can include terms of the form X1*X2*(X1 – X2), which are called Scheffé cubic terms.
Scheffé cubic terms are also included if you enter a 3 in the Degree box and then select the Mixture Response Surface macro command.
 Grouped Regressors
Grouped Regressors
Creates a single effect for a set of continuous factors that are treated as one effect in various parts of the report. You can add or remove the grouped effect in the Effect Summary. There is one leverage plot and one effect test for each group effect, rather than individual plots and tests for each factor in the group. This can be useful if your data table contains indicator columns that represent levels of a categorical effect.
Note: Non-continuous factors included in a group of regressors are not included in the analysis.
Attributes
In the Attributes list, select attributes that you can assign to an effect selected in the Construct Model Effects list.
Random Effect
Assigns the Random attribute to an effect. For more information about random effects, see Specifying Random Effects and Fitting Method.
Response Surface Effect
Assigns the RS attribute to an effect. Note that the relevant model terms must be included in the Construct Model Effects list. The Response Surface option in the Macros list automatically generates these terms and assigns the RS attribute to the main effects. To obtain the Response Surface report, interaction and polynomial terms do not need to have the RS attribute assigned to them. You need only assign this attribute to main effects.
LogVariance Effect
Assigns the LogVariance attribute to an effect. This attribute indicates that the effect is to be included in a model of the variance of the response.
To include an effect in models for both the mean and variance of the response, you must specify the effect twice. In the tabbed interface, it must appear on both the Mean Effects and Variance Effects tabs. Otherwise, you can enter it twice on the Mean Effects tab, once without the LogVariance Effect attribute and once with the LogVariance Effect attribute.
Mixture Effect
Assigns the Mixture attribute to main effects. This is used to specify the main effects involved in the mixture. Note that the Mixture Response Surface option in the Macros list automatically assigns the mixture attribute to selected effects, and provides a Response Surface report when possible.
Excluded Effect
Assigns the Excluded attribute to an effect. This excludes the effect from the model fit. However, the effect is used to group observations for lack-of-fit tests. In the Standard Least Squares personality, a table of least square means is provided for this effect.
Knotted Spline Effect
Assigns the Knotted attribute to a continuous main effect. This implicitly adds cubic splines for the effect to the model specification. See Knotted Spline Effect.
Knotted Spline Effect
Knotted splines are used to fit a response Y using a flexible function of a predictor. Consider the single predictor X. When the Knotted Spline Effect is assigned to X, and k knots are specified, then k - 2 additional effects are implicitly added to the set of predictors. Each of these effects is a piecewise cubic polynomial spline whose segments are defined by the knots. See Stone and Koo (1985).
The number of splines is determined by the number of knots, which you are asked to specify. The coefficients associated with the splines are estimated based on the method used by the personality.
The placement of knots follows guidance given in the literature. In particular, if there are 100 or fewer points, the first and last knots are the fifth smallest and largest points, respectively. Otherwise, the first and last knots are placed at the 0.05 and 0.95 quantiles for 5 or fewer knots, or the 0.025 and 0.975 quantiles for more than 5 knots. The default number of knots is 5 for more than 30 observations, and 3 for fewer than 30 observations.
Note: Knotted splines are implemented only for main-effect continuous terms.
Transform
The Transform options transform selected Y columns or main effects that are selected in the Construct Model Effects text box.
Note: You can also transform a column by right-clicking it in the Select Columns list and selecting Transform. A reference to the transformed column appears in the Select Columns list. You can then use the column in the Fit Model window as you would any data table column. See Transform Columns in a JMP Platform in Using JMP.
None
Removes any Transform options that have been applied.
Log
Applies the natural logarithm transformation to the selected variable.
Sqrt
Applies the square root of the values of the selected variable.
Square
Applies the square of the values of the selected variable.
Reciprocal
Applies the transformation 1/X to the variable X.
Exp
Applies the exponential transformation to the selected variable.
Arrhenius
Applies the Arrhenius transformation to the variable T (temperature in degrees Centigrade):
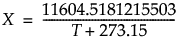
This is the component of the Arrhenius relationship that is multiplied by the activation energy.
ArrheniusInv
Applies the inverse of the Arrhenius transformation to the variable X:
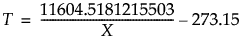
Logit
Calculates the inverse of the logistic function for the selected column (where p is in the range of 0 to 1):
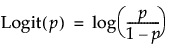
Logistic
Calculates the logistic (also known as Squish and Logist) function for the selected column (where the result is in the range of 0 to 1):
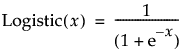
LogitPct
Calculates the logit as a percent for the selected column (where pct is a percent in the range of 0 to 100):
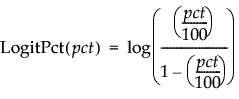
LogisticPct
Calculates the logistic (or logist) as a percent for the selected column (where the result is in the range of 0 to 100):
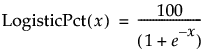
No Intercept
Select No Intercept if you want to fit a model with no intercept term. Certain modeling structures require no intercept models. For these, the No Intercept box is checked by default.
Construct Model Effects Tabs
For the following personalities, you can enter model effects using a tabbed interface:
Note: If you apply Attributes to effects on the first (main) tab, the attributes determine how the effects are treated in the model. If you run the model and then request Model Dialog from the report’s red triangle menu, you find that those effects appear on the appropriate tabs.
Standard Least Squares
Enter model effects:
Fixed Effects tab
Enter effects to be modeled as fixed effects. A fixed effect is one whose specific treatment levels are of interest. You want to compare the mean response across its treatment levels.
Random Effects tab
Enter effects to be modeled as random effects. A random effect is one whose levels are considered a random sample from a larger population. You want to estimate the variation in the response that is attributable to this effect.
Mixed Model
Enter model effects:
Fixed Effects tab
Enter effects to be modeled as fixed effects. See Standard Least Squares in this table.
Random Effects tab
Enter effects to be modeled as random effects. Use for variance component models and random coefficients models.
Repeated Structure tab
Use to select a covariance structure for repeated effects.
Loglinear Variance
Enter model effects:
Mean Effects tab
Enter effects for which you want to model expected values.
Variance Effects tab
Enter effects for which you want to model variance.
If you want to model both the expected value and variance of an effect, you must enter it on both tabs.
Parametric Survival
Enter model effects:
Location Effects tab
Enter effects that you want to use in modeling the location parameter, mu, or in the case of the Weibull distribution, the shape parameter.
Scale Effects tab
Enter effects that you want to use in modeling the scale parameter.