Discriminant Methods
JMP offers these methods for conducting Discriminant Analysis: Linear, Quadratic, Regularized, and Wide Linear. The first three methods differ in terms of the underlying model. The Wide Linear method is an efficient way to fit a Linear model when the number of covariates is large.
Note: When you enter more than 500 covariates, a JMP Alert recommends that you switch to the Wide Linear method. This is because computation time can be considerable when you use the other methods with a large number of columns. Click Wide Linear, Many Columns to switch to the Wide Linear method. Click Continue to use the method you originally selected.
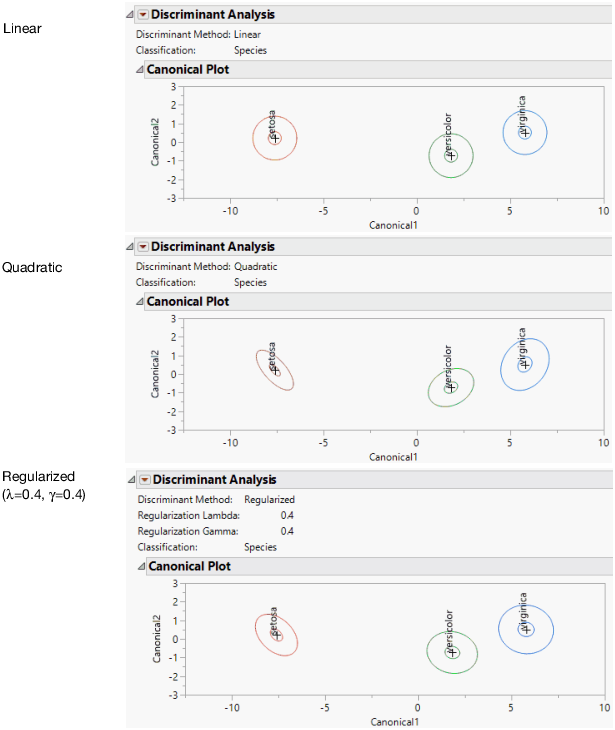
Figure 5.7 Linear, Quadratic, and Regularized Discriminant Analysis
The Linear, Quadratic, and Regularized methods are illustrated in Figure 5.7. The methods are described here briefly. See Saved Formulas.
Linear, Common Covariance
Performs linear discriminant analysis. This method assumes that the within-group covariance matrices are equal. See Linear Discriminant Method.
Quadratic, Different Covariances
Performs quadratic discriminant analysis. This method assumes that the within-group covariance matrices differ. This method requires estimating more parameters than the Linear method requires. If group sample sizes are small, you risk obtaining unstable estimates. See Quadratic Discriminant Method.
If a covariate is constant across a level of the X variable, then its related entries in the within-group covariance matrix have zero covariances. To enable matrix inversion, the zero covariances are replaced with the corresponding pooled within covariances. When this is done, a note appears in the report window identifying the problematic covariate and level of X.
Tip: A shortcoming of the quadratic method surfaces in small data sets. It can be difficult to construct invertible and stable covariance matrices. The Regularized method ameliorates these problems, still allowing for differences among groups.
Regularized, Compromise Method
Provides two ways to impose stability on estimates when the within-group covariance matrices differ. This is a useful option when group sample sizes are small. See Regularized, Compromise Method and Regularized Discriminant Method.
Wide Linear, Many Columns
Useful in fitting models based on a large number of covariates, where other methods can have computational difficulties. This method assumes that all within-group covariance matrices are equal. This method uses a singular value decomposition approach to compute the inverse of the pooled within-group covariance matrix. See Description of the Wide Linear Algorithm.
Note: When you use the Wide Linear option, a few of the features that normally appear for other discriminant methods are not available. This is because the algorithm does not explicitly calculate the very large pooled within-group covariance matrix.
Regularized, Compromise Method
Regularized discriminant analysis is governed by two nonnegative parameters.
• The first parameter (Lambda, Shrinkage to Common Covariance) specifies how to mix the individual and group covariance matrices. For this parameter, 1 corresponds to Linear Discriminant Analysis and 0 corresponds to Quadratic Discriminant Analysis.
• The second parameter (Gamma, Shrinkage to Diagonal) is a multiplier that specifies how much deflation to apply to the non-diagonal elements (the covariances across variables). If you choose 1, then the covariance matrix is forced to be diagonal.
Assigning 0 to each of these two parameters is identical to requesting quadratic discriminant analysis. Similarly, assigning 1 to Lambda and 0 to Gamma requests linear discriminant analysis. Use Table 5.1 to help you decide on the regularization. See Figure 5.7 for examples of linear, quadratic, and regularized discriminant analysis.
Use Smaller Lambda | Use Larger Lambda | Use Smaller Gamma | Use Larger Gamma |
|---|---|---|---|
Covariance matrices differ | Covariance matrices are identical | Variables are correlated | Variables are uncorrelated |
Many rows | Few rows |
|
|
Few variables | Many variables |
|
|