Estimation Methods
REML
REML (restricted maximum likelihood) estimates are less biased than the ML (maximum likelihood) estimation method when the data contains missing values. The REML method maximizes marginal likelihoods based on error contrasts. The REML method is often used for estimating variances and covariances. The REML method in the Principal Components platform is the same as the REML estimation of mixed models for repeated measures data with an unstructured covariance matrix. See the documentation for SAS PROC MIXED about REML estimation of mixed models.
Wide
The Wide method uses a computationally efficient algorithm that avoids calculating the covariance matrix. The algorithm is based on the singular value decomposition. Consider the following notation:
• n = number of rows
• p = number of variables
• X = n by p matrix of data values
The number of nonzero eigenvalues, and consequently the number of principal components, equals the rank of the correlation matrix of X. The number of nonzero eigenvalues cannot exceed the smaller of n and p.
When you select the Wide method, the data are standardized. To standardize a value, subtract its mean and divide by its standard deviation. Denote the n by p matrix of standardized data values by Xs. Then the covariance matrix of the standardized data is the correlation matrix of X and it is defined as follows:
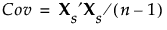
Using the singular value decomposition, Xs is written as UDiag(Λ)V′. This representation is used to obtain the eigenvectors and eigenvalues of Xs′Xs. The principal components, or scores, are given by XsV. For additional background information, see Wide Linear Methods and the Singular Value Decomposition.
 Sparse
Sparse
Similar to the Wide method, the Sparse method is based on singular value decomposition. Therefore, the algorithm for the Sparse method avoids computing the covariance matrix and is computationally efficient.
Consider the same notation and standardization of X that is described in Wide. The correlation matrix of X is represented by the covariance matrix of Xs:
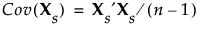
The Sparse method differs from the Wide method in the calculation of the singular value decomposition. The Wide method performs a full singular value decomposition. However, the Sparse method uses an algorithm that computes only the first specified number of singular values and singular vectors in the singular value decomposition. Therefore, only the first specified number of eigenvalues and principal components are returned. For more information about the algorithm, see Baglama and Reichel (2005).