Example of MSA Design
In this example, you want to study the variability in your measurement system due to instruments and operators. You have two scales in your lab and four operators who have time to participate in the study. You have a set of five standard parts to weigh and each operator makes six measurements per part per instrument. You do not have previous estimates of variability, so you design an experiment based on a variance of one, which results in diagnostics that are scaled to the true variability.
1. Select DOE > Special Purpose > MSA Design.
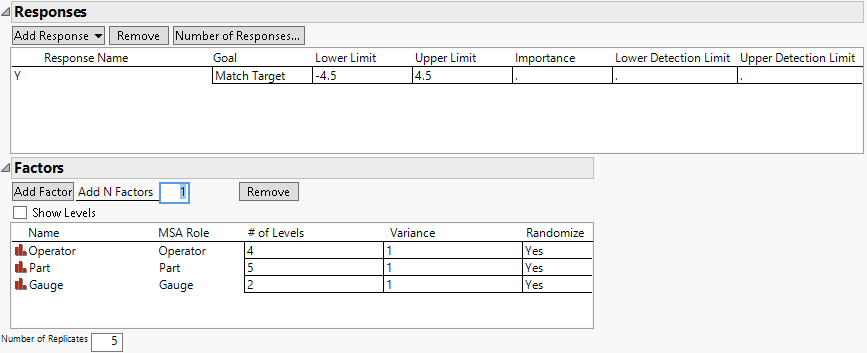
2. Set the Goal for the response Y, to Match Target.
3. Set the # of Levels for Operator to 4.
4. Set the # of Levels for Part to 5.
5. Set the # of Levels for Gauge to 2.
6. Set the Number of Replicates to 5 to include 6 measurements for each design run.
Figure 25.2 Factor Settings
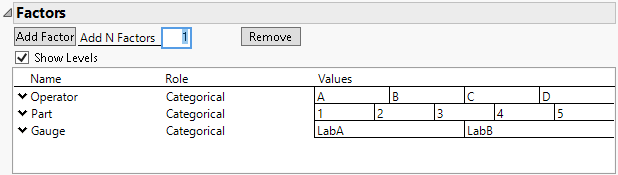
7. Select Show Levels.
8. Edit the factor Values as shown in Figure 25.3.
Figure 25.3 Factor Values
Note: Setting the Random Seed in step 9 reproduces the design and diagnostics shown in this example.
9. (Optional) Click the MSA red triangle, select Set Random Seed, type 123.
10. Click Make Design.
Note: Click Make Table to generate a table for data collection. See MSA Design Table for analysis scripts that are included in the design table.
11. Scroll down to the Design Diagnostics outline and click the gray disclosure icon to open.
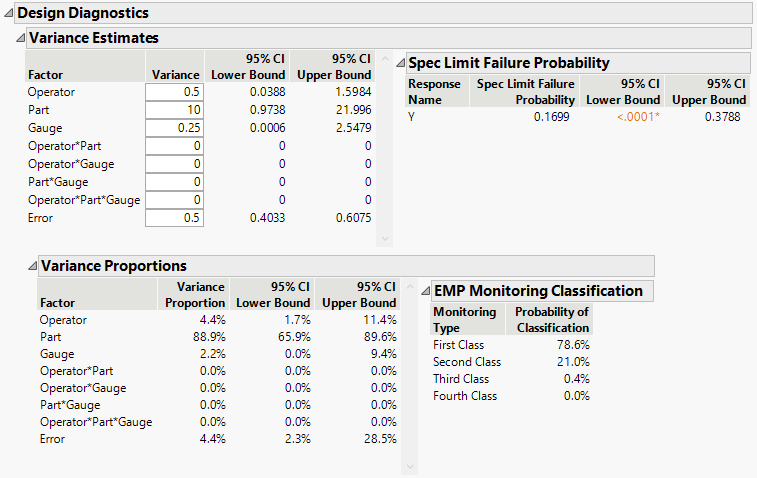
The Design Diagnostics report contains settings for assumed variances that are then used to estimate confidence intervals, variance proportions and EMP Monitoring Classifications. These estimates are used to evaluate the strength of your MSA study design. Explore different variance assumptions, or use the Back button to make adjustments to your design.
12. Adjust the expected Variance of your factors to explore the impact on your design diagnostics. Set Operator Variance to 0.5, Part Variance to 10, and Gauge Variance to 0.25.
Figure 25.4 MSA Design Diagnostics
All diagnostics are based on simulations that are computed from the sampling distributions of the appropriate mean squares. Based on the variance estimate assumptions the study results in a 78% probability of a first class process.