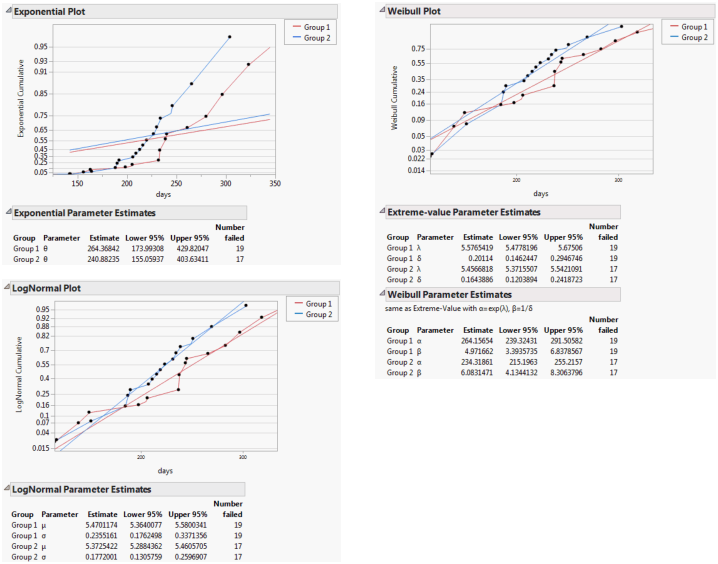
Exponential, Weibull, and Lognormal Plots and Fits
For each of the three supported distributions in the Survival platform, there is a plot command and a fit command. Use the plot command to see whether the event markers seem to follow a straight line. The markers tend to follow a straight line when the distributional fit is suitable for the data. Then, use the fit commands to estimate the parameters.
Figure 13.5 Exponential, Weibull, and Lognormal Plots and Reports
The following table shows what to plot to make a straight line fit for that distribution:
Distribution Plot | Horizontal Axis | Vertical Axis | Interpretation |
|---|---|---|---|
Exponential | time | -log(S) | slope is 1/theta |
Weibull | log(time) | log(-log(S)) | slope is beta |
Lognormal | log(time) | Probit(1-S) | slope is 1/sigma |
Note: S = product-limit estimate of the survival distribution.
Exponential
The exponential distribution is the simplest distribution for modeling time-to-event data. The exponential distribution has only one parameter, theta. It is a constant-hazard distribution, with no memory of how long it has survived to affect how likely an event is. The parameter theta is the expected lifetime.
Weibull
The Weibull distribution is the most popular distribution for modeling time-to-event data. The Weibull distribution can have two or three parameters. The Survival platform fits the two-parameter Weibull distribution. Authors parameterize this distribution in many different ways (Table 13.2). JMP reports two of these parameterizations: the Weibull alpha-beta parameterization and a parameterization based on the smallest extreme value distribution.
The alpha-beta parameterization, shown in the Weibull Parameter Estimates report, is widely used in the reliability literature (Nelson 1990). The alpha parameter is interpreted as the quantile at which 63.2% of the units fail. The beta parameter determines how the hazard rate changes over time. If beta > 1, the hazard rate increases over time; if beta < 1, the hazard rate decreases over time; and if beta = 1, the hazard rate is constant over time. A Weibull distribution with a constant hazard function is equivalent to an exponential distribution.
The lambda-delta extreme value parameterization is shown in the Extreme-Value Parameter Estimates report. This parameterization is sometimes desirable in a statistical sense because it places the Weibull distribution in a location-scale setting (Meeker and Escobar 1998, p. 86). The location parameter is lambda, and the scale parameter is delta. In relation to the alpha-beta parameterization, lambda is equal to the natural log of alpha, and delta is equal to the reciprocal of beta. Therefore, the delta parameter determines how the hazard rate changes over time. If delta > 1, the hazard rate decreases over time; if delta < 1, the hazard rate increases over time; and if delta = 1, the hazard rate is constant over time. A Weibull distribution with a constant hazard function is equivalent to an exponential distribution.
JMP Weibull | alpha | beta |
Wayne Nelson | alpha=alpha | beta=beta |
Meeker and Escobar | eta=alpha | beta=beta |
Tobias and Trindade | c = alpha | m = beta |
Kececioglu | eta=alpha | beta=beta |
Hosmer and Lemeshow | exp(X beta)=alpha | lambda=beta |
Blishke and Murthy | beta=alpha | alpha=beta |
Kalbfleisch and Prentice | lambda = 1/alpha | p = beta |
JMP Extreme Value | lambda=log(alpha) | delta=1/beta |
Meeker and Escobar s.e.v. | mu=log(alpha) | sigma=1/beta |
Lognormal
The lognormal distribution is also very popular for modeling time-to-event data. The lognormal distribution is equivalent to the distribution where if you take the log of the values, the distribution is normal. If you want to fit a normal distribution to your data, you can take the exp() of it and model your data with a lognormal distribution. See Additional Examples of Fitting Parametric Survival.
Additional Options
To see additional options for the exponential, Weibull, and lognormal fits, press Shift, click the red triangle next to Product-Limit Survival Fit, and select the desired fit.
Use these options to do the following tasks:
• Set the confidence level for the limits.
• Set the constrained value for theta (in the case of an exponential fit), sigma (in the case of a lognormal fit) or beta (in the case of a Weibull fit). See WeiBayes Analysis.
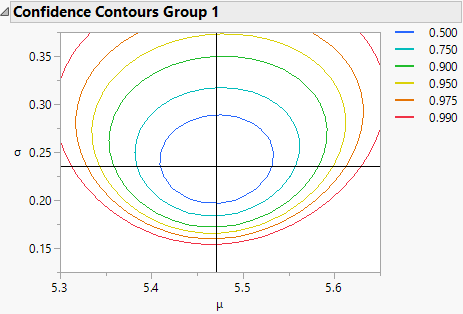
• Obtain a Confidence Contour Plot for the Weibull and lognormal fits (when there are no constrained values).
Figure 13.6 Confidence Contour Plot
WeiBayes Analysis
JMP can constrain the values of the Theta (Exponential), Beta (Weibull), and Sigma (LogNormal) parameters when fitting these distributions. This feature is needed in WeiBayes situations, for example:
• Where there are few or no failures
• There are existing historical values for beta
• There is still a need to estimate alpha
For more information about WeiBayes situations, see Abernethy (1996).
With no failures, the standard technique is to add a failure at the end. Then, the estimates reflect a type of lower bound on the alpha value, rather than a real estimate. However, the WeiBayes feature allows for a true estimation.