Spatial and Temporal Variability
Consider the simple model yi = μ + ei. The spatial or temporal structure is modeled through the error term, ei. In general, the spatial correlation model can be defined as Var(ei) = σi2 and Cov(ei, ej) = σij.
Let si denote the location of yi, where si is specified by coordinates reflecting space or time. The spatial or temporal structure is typically restricted by assuming that the covariance is a function of the Euclidean distance, dij, between si and sj. The covariance can be written as Cov(ei, ej) = σ2[f(dij)], where f(dij) represents the correlation between observations yi and yj.
In the case of two or more location coordinates, if f(dij) does not depend on direction, then the covariance structure is isotropic. If it does, then the structure is anisotropic.
Spatial Correlation Structure
The correlation structures for spatial models available in JMP are shown below. These are parametrized by ρ, which is positive unless it is otherwise constrained.
• Spherical
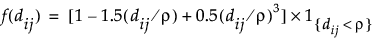
where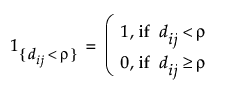 
• Exponential
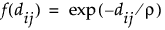
• Gaussian
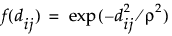
• Power
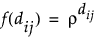
For an anisotropic model, the correlation function contains a parameter, ρκ, for each direction.
Variogram
When the spatial process is second-order stationary, the structures listed in Spatial Correlation Structure define variograms. Borrowed from geostatistics, the variogram is the standard tool for describing and estimating spatial variability. It measures spatial variability as a function of the distance, dij, between observations using the semivariance.
Let Z(s) denote the value of the response at a location s. The semivariance between observations at si and sj is defined as follows:
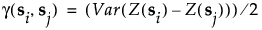
If the response has a constant mean, then the expression can be simplified to the following:
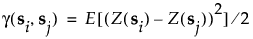
If the process is isotropic, the semivariance depends only on the distance h between points and the function can be specified as follows:
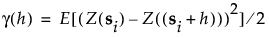
The following terms are associated with variograms:
Nugget
Defined as the intercept. This represents a jump discontinuity at h = 0.
Sill
Defined as the value of the semivariogram at the plateau reached for larger distances. It corresponds to the variance of an observation. In models with no nugget effect, the sill is σ2. In models with a nugget effect, the sill is σ2 + c1, where c1 represents the nugget. The partial sill is defined as σ2.
Range
Defined as the distance at which the semivariogram reaches the sill. At distances less than the range, observations are spatially correlated. For distances greater than or equal to the range, spatial correlation is effectively zero. In spherical models, ρ is the range. In exponential models, 3ρ is the practical range. In Gaussian models,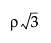 
is the practical range. The practical range is defined as the distance where covariance is reduced to 95% of the sill.
In Figure 8.34, the repeated effects covariance parameter estimates represent the various semivariogram features:
Spatial Spherical
An estimate of the range, ρ.
Nugget
A scaled estimate of c1. The Residual times the Nugget is c1.
Residual
The partial sill or the sill in no nugget models.
Variogram Estimate
For a given isotropic spatial structure, the estimated variogram is obtained using a nonlinear least squares fit of the observed data to the appropriate function in Spatial Correlation Structure.
Empirical Semivariance
To compute the empirical semivariance, the distances between all pairs of points for the variables selected for the variogram covariance are computed. The range of the distances is divided into 10 equal intervals. If the data do not allow for 10 intervals, then as many intervals as possible are constructed.
Distance classes consisting of pairs of points are constructed. The hth distance class consists of all pairs of points whose distances fall in the hth interval.
Consider the following notation:
n
total number of pairs of points
Ch
distance class consisting of points whose distance falls into the hth largest interval
Z(x)
value of the response at x, where x is a vector of temporal or spatial coordinates
γ(h)
semivariance for distance class Ch
The semivariance function, γ, is defined as follows:
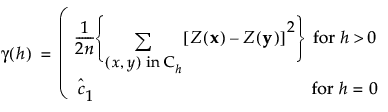
Here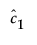 
is an estimate of the nugget effect.