Uplift Model Graph
Uplift Model Graph
The graph represents the response on the vertical axis. The horizontal axis corresponds to observations, arranged by nodes. For each node, a black horizontal line shows the mean response. Within each split, there is a subsplit for treatment shown by a red or blue line. These lines indicate the mean responses for each of the two treatment groups within the split. The value ordering of the treatment column determines the placement order of these lines. As nodes are split, the graph updates to show the splits beneath the horizontal axis. Vertical lines divide the splits.
Beneath the graph are the control buttons: Split, Prune, and Go. The Go button appears only if there is a validation set. Also shown is the name of the Treatment column and its two levels, called Treatment1 and Treatment2. If more than two levels are specified for the Treatment column, all levels except the first are treated as a single level and combined into Treatment2.
To the right of the Treatment column information is a report showing summary values relating to prediction. (Keep in mind that prediction is not the objective in uplift modeling.) The report updates as splitting occurs. If a validation set is used, values are shown for both the training and the validation sets.
RSquare
The RSquare for the regression model associated with the tree. Note that the regression model includes interactions with the treatment column. An RSquare closer to 1 indicates a better fit to the data than does an RSquare closer to 0.
Note: A low RSquare value suggests that there might be variables not in the model that account for the unexplained variation. However, if your data are subject to a large amount of inherent variation, even a useful uplift model can have a low RSquare value.
RMSE
The root mean square error (RMSE) for the regression model associated with the tree. RMSE is given only for continuous responses. See Fitting Linear Models.
N
The number of observations.
Number of Splits
The number of times splitting has occurred.
AICc
The Corrected Akaike Information Criterion (AICc), computed using the associated regression model. AICc is given only for continuous responses. See Likelihood, AICc, and BIC in Fitting Linear Models.
 Uplift Decision Tree
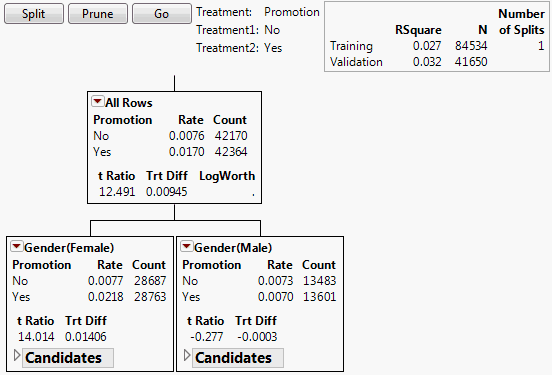
Uplift Decision Tree
The decision tree shows the splits used to model uplift. See Figure 6.5 for an example using the Hair Care Product.jmp sample data table. Each node contains the following information:
Treatment
The name of the treatment column is shown, with its two levels.
Rate
(Appears only for two-level categorical responses.) For each treatment level, the proportion of subjects in this node who responded.
Mean
(Appears only for continuous responses.) For each treatment level, the mean response for subjects in this node.
Count
The number of subjects in this node in the specified treatment level.
t Ratio
The t ratio for the test for a difference in response across the levels of Treatment for subjects in this node. If the response is categorical, it is treated as continuous (values 0 and 1) for this test.
Trt Diff
The difference in response means across the levels of Treatment. This is the uplift, with the following assumptions:
– The first level in the treatment column’s value ordering represents the treatment.
– The response is defined so that larger values reflect greater impact.
LogWorth
The value of the logworth for the subsequent split based on the given node.
Figure 6.5 Nodes for First Split
Candidates Report
Each node also contains a Candidates report with additional information:
Term
The model term.
LogWorth
The maximum logworth over all possible splits for the given term. The logworth corresponding to a split is -log10 of the adjusted p-value.
F Ratio
When the response is continuous, this is the F Ratio associated with the interaction term in a linear regression model. The regression model specifies the response as a linear function of the treatment, the binary split, and their interaction. When the response is categorical, this is the ChiSquare value for the interaction term in a nominal logistic model.
Gamma
When the response is continuous, this is the coefficient of the interaction term in the linear regression model used in computing the F ratio. When the response is categorical, this is an estimate of the interaction constructed from Firth-adjusted log-odds ratios.
Cut Point
If the term is continuous, this is the point that defines the split. If the term is categorical, this describes the first (left) node.