Evaluating Power Relative to a Specified Model
For this example, you have constructed a definitive screening design to determine which of six factors have an effect on the yield of an extraction process. The data are given in the Extraction Data.jmp sample data table, located in the Design Experiment folder. Because the design is a definitive screening design, each factor has three levels. See Definitive Screening Designs.
You are interested in the power of tests to detect a strong quadratic effect. You consider a strong effect to be one whose magnitude is at least three times as large as the error variation.
Although the experiment studies six factors, effect sparsity suggests that only a small subset of factors is active. Consequently, you feel comfortable investigating power in a model based on a smaller number of factors. Also, past studies on a related process provide strong evidence to suggest that three of the factors, Propanol, Butanol, and pH, have negligible main effects, do not interact with other factors, and do not have quadratic effects. This leads you to believe that the likely model contains main, interaction, and quadratic effects only for Methanol, Ethanol, and Time. You decide to investigate power in the context of a three-factor response surface model.
Use the Evaluate Design platform to determine the power of your design to detect strong quadratic effects for Methanol, Ethanol, or Time.
1. Select Help > Sample Data Library and open Design Experiment/Extraction Data.jmp.
2. Select DOE > Design Diagnostics > Evaluate Design.
3. Select Methanol, Ethanol, and Time and click X, Factor.
You can add Yield as Y, Response if you wish. But specifying the response has no effect on the properties of the design.
4. Click OK.
5. In the Model outline, click RSM.
This adds the interaction and quadratic terms for the three factors.
6. Open the Power Analysis outline.
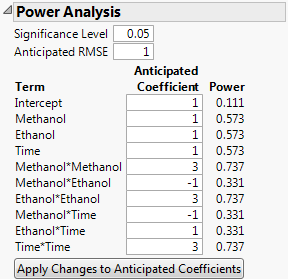
Note that the Anticipated RMSE is set to 1 by default. Although you have an estimate of the RMSE from past studies, you need not enter it. This is because the magnitude of the effect of interest is three times the error variation.
7. Under Anticipated Coefficient, type 3 next to Methanol*Methanol, Ethanol*Ethanol, and Time*Time.
8. Click Apply Changes to Anticipated Coefficients.
Figure 15.9 Power Analysis Outline after Applying Changes to Coefficients
The power of detecting a quadratic effect whose magnitude is three times the error variation is 0.737. This assumes a final model that is a response surface in three factors. It also assumes a 0.05 significance level for the test.