Experiments for Robust Process and Product Design
Often processes or products are impacted by noise factors. These are factors that are not easy or cost effective to control. Finding process or product settings of controllable factors that are least impacted by noise factors is desirable. Historically, Taguchi designs provided a method for experimenting in the presence of noise factors. Note that noise factors must be controlled during an experiment.
Alternatives to Taguchi designs include combined arrays and mixed resolution designs (Borror and Montgomery, 2000). The mixed resolution designs are used to obtain designs that contain both control and noise factors. The goal of such a design is to find robust settings for control variables. The key is the ability to estimate specific effects. In particular, one is interested in estimating main effects of the control variables, main effects of the noise variables, control by control interactions, noise by control interactions, and quadratic terms for the control variables.
Use the custom designer to generate a design for studying robust process settings.
In this example, you are interested in finding optimal settings for four control settings in the presence of three noise factors.
1. Select DOE > Custom Design.
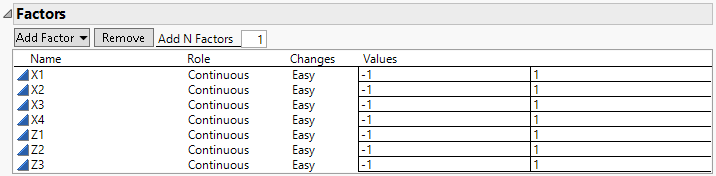
2. In the Factors outline, type 4 next to Add N Factors.
3. Click Add Factor > Continuous.
4. In the Factors outline, type 3 next to Add N Factors.
5. Click Add Factor > Continuous.
6. Double-click X5 and change it to Z1 to designate a noise factor. Repeat to change X6 and X7 to Z2 and Z3.
Figure 5.83 Factor Outline for Design with 4 Control and 3 Noise Factors
7. Click Continue.
Next you set up the model that for exploring optimal settings for the control factors that are least impacted by the noise factors.
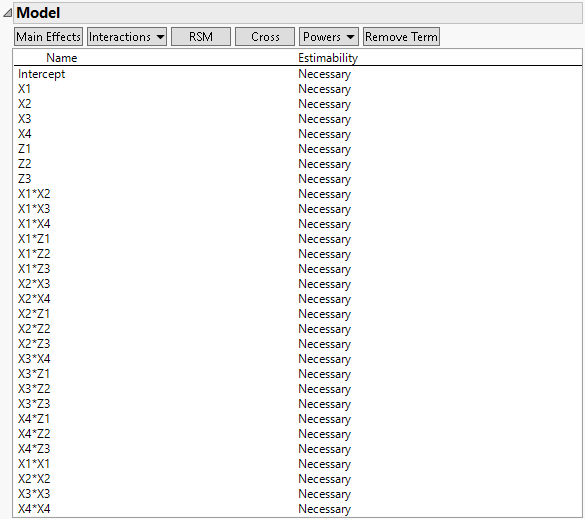
8. The model contains all main effects by default.
9. Click Interactions > 2nd to add all two-way interactions.
This enters the control by control interactions, the control by noise interactions, and the noise by noise interactions. You do not want to estimate the interaction between noise factors.
10. Scroll to the bottom of the list, highlight Z1*Z2, Z1*Z3, and Z2*Z3 and click Remove Term.This removes the noise by noise interactions.
11. In the Factors outline, select X1, X2, X3, and X4.
12. In the Model outline, click Powers > 2nd to add the control variable quadratic terms.
Figure 5.84 Model Outline for Design with Noise Factors
13. Add two center points by entering 2 In the Number of Center Points: text box
14. Click Make Design.
The result is a 36 run design that enables you to evaluate and optimize your control factors in the presence of your three noise factors. The goal of your analysis is to determine which effects are important and then to select settings for the control factors that are least impacted by the noise factors.