Gaussian Process IMSE Optimal Designs
The Gaussian process IMSE optimal design method constructs designs that are suitable for Gaussian process models. Gaussian process models fit a wide variety of surfaces. Gaussian process IMSE optimal designs minimize the integrated mean squared error of the Gaussian process model over the experimental region. The Gaussian process IMSE optimal design method uses a correlation structure similar to that of the kriging model. See Jones and Johnson (2009).
Covariance Parameter Vector
In a Gaussian Process IMSE Optimal Design formulation of the Gaussian process model, the covariance parameter vector determines the correlation structure. There is a Theta for each factor. A theta equal to 0 corresponds to a correlation of 1, causing the fitted surface to be flat in the corresponding factor’s direction. As theta increases, the correlation decreases, allowing the surface to be flexible in the factor’s direction.
In the Covariance Parameter Vector outline, in the list of values under Thetas, you can enter values that reflect your prior knowledge of the surface.
Comparison of Gaussian Process IMSE Optional Design with Latin Hypercube Design
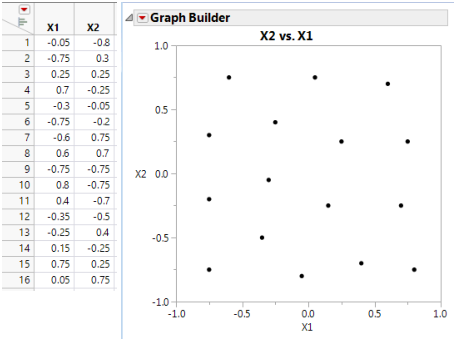
Gaussian process IMSE optimal designs are alternatives to the Latin Hypercube design. You can compare the IMSE optimal design to the Latin Hypercube (shown previously in Figure 21.20). The table and overlay plot in Figure 21.22 show a Gaussian IMSE optimal design. You can see that the design provides uniform coverage of the factor region.
Figure 21.22 Comparison of Two-factor Latin Hypercube and Gaussian IMSE Optimal Designs
Note: Both the Maximum Entropy design and the Gaussian Process IMSE Optimal design were created using 100 random starts.