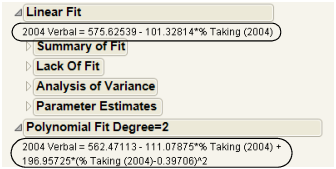
Linear Fit and Polynomial Fit Reports

The Linear Fit and Polynomial Fit reports begin with the equation of fit.

Figure 5.9 Example of Equations of Fit 

Tip: You can edit the equation by clicking on it.

Each Linear and Polynomial Fit Degree report contains at least three reports. A fourth report, Lack of Fit, appears only if there are X replicates in your data.

Summary of Fit Report

The Summary of Fit reports in the Bivariate platform show the numeric summaries of the response for the linear fit and polynomial fit of degree 2 for the same data. You can compare multiple Summary of Fit reports to see the improvement of one model over another, indicated by a larger RSquare value and smaller Root Mean Square Error.

Figure 5.10 Summary of Fit Reports for Linear and Polynomial Fits 

The Summary of Fit report contains the following columns:

RSquare

Measures the proportion of the variation explained by the model. The remaining variation is not explained by the model and attributed to random error. The RSquare is 1 if the model fits perfectly.

Note: A low RSquare value suggests that there might be variables not in the model that account for the unexplained variation. However, if your data are subject to a large amount of inherent variation, even a useful regression model can have a low RSquare value. Read the literature in your research area to learn about typical RSquare values.

The RSquare values in Figure 5.10 indicate that the polynomial fit of degree 2 gives a small improvement over the linear fit. See Summary of Fit Report.

RSquare Adj

Adjusts the RSquare value to make it more comparable over models with different numbers of parameters by using the degrees of freedom in its computation. See Summary of Fit Report.

Root Mean Square Error

Estimates the standard deviation of the random error. It is the square root of the mean square for Error in the Analysis of Variance report (Figure 5.12).

Mean of Response

Provides the sample mean (arithmetic average) of the response variable. This is the predicted response when no model effects are specified.

Observations

Provides the number of observations used to estimate the fit. If there is a weight variable, this is the sum of the weights.

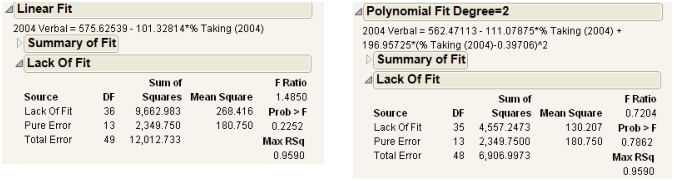
Lack of Fit Report

Note: The Lack of Fit report appears only if there are multiple rows that have the same x value.

Using the Lack of Fit report, you can estimate the error, regardless of whether you have the right form of the model. This occurs when multiple observations occur at the same x value. The error that you measure for these exact replicates is called pure error. This is the portion of the sample error that cannot be explained or predicted no matter what form of model is used. However, a lack of fit test might not be of much use if it has only a few degrees of freedom for it (few replicated x values).

Figure 5.11 Examples of Lack of Fit Reports for Linear and Polynomial Fits 

The difference between the residual error from the model and the pure error is called the lack of fit error. The lack of fit error can be significantly greater than the pure error if you have the wrong functional form of the regressor. In that case, you should try a different type of model fit. The Lack of Fit report tests whether the lack of fit error is zero.

The Lack of Fit report contains the following columns:

Source

The three sources of variation: Lack of Fit, Pure Error, and Total Error.

DF

The degrees of freedom (DF) for each source of error.

– The Total Error DF is the degrees of freedom found on the Error line of the Analysis of Variance table (shown under the Analysis of Variance Report). It is the difference between the Total DF and the Model DF found in that table. The Error DF is partitioned into degrees of freedom for lack of fit and for pure error.

– The Pure Error DF is pooled from each group where there are multiple rows with the same values for each effect. See Lack of Fit Report.

– The Lack of Fit DF is the difference between the Total Error and Pure Error DF.

Sum of Squares

The sum of squares (SS for short) for each source of error.

– The Total Error SS is the sum of squares found on the Error line of the corresponding Analysis of Variance table, shown under Analysis of Variance Report.

– The Pure Error SS is pooled from each group where there are multiple rows with the same value for the x variable. This estimates the portion of the true random error that is not explained by model x effect. See Lack of Fit Report.

– The Lack of Fit SS is the difference between the Total Error and Pure Error sum of squares. If the lack of fit SS is large, the model might not be appropriate for the data. The F-ratio described below tests whether the variation due to lack of fit is small enough to be accepted as a negligible portion of the pure error.

Mean Square

The sum of squares divided by its associated degrees of freedom. This computation converts the sum of squares to an average (mean square). F-ratios for statistical tests are the ratios of mean squares.

F Ratio

The ratio of mean square for lack of fit to mean square for Pure Error. It tests the hypothesis that the lack of fit error is zero.

Prob > F

The probability of obtaining a greater F-value if the variation due to lack of fit variance and the pure error variance are the same. A high p-value means that there is not a significant lack of fit.

Max RSq

The maximum R2 that can be achieved by a model using only the variables in the model. See Lack of Fit Report.

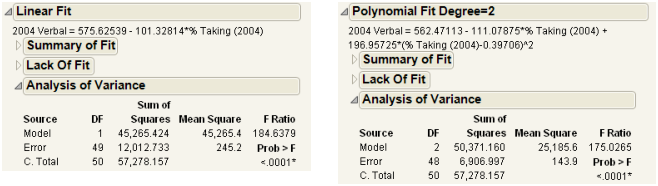
Analysis of Variance Report

Analysis of variance (ANOVA) for a regression partitions the total variation of a sample into components. These components are used to compute an F-ratio that evaluates the effectiveness of the model. If the probability associated with the F-ratio is small, then the model is considered a better statistical fit for the data than the response mean alone.

The Analysis of Variance reports in Figure 5.12 compare a linear fit (Fit Line) and a second degree (Fit Polynomial). Both fits are statistically better from a horizontal line at the mean.

Figure 5.12 Examples of Analysis of Variance Reports for Linear and Polynomial Fits 

The Analysis of Variance Report contains the following columns:

Source

The three sources of variation: Model, Error, and C. Total.

DF

The degrees of freedom (DF) for each source of variation:

– A degree of freedom is subtracted from the total number of nonmissing values (N) for each parameter estimate used in the computation. The computation of the total sample variation uses an estimate of the mean. Therefore, one degree of freedom is subtracted from the total, leaving 50. The total corrected degrees of freedom are partitioned into the Model and Error terms.

– One degree of freedom from the total (shown on the Model line) is used to estimate a single regression parameter (the slope) for the linear fit. Two degrees of freedom are used to estimate the parameters (β1 and β2) for a polynomial fit of degree 2.

– The Error degrees of freedom is the difference between C. Total df and Model df.

Sum of Squares

The sum of squares (SS for short) for each source of variation:

– In this example, the total (C. Total) sum of squared distances of each response from the sample mean is 57,278.157, as shown in Figure 5.12. That is the sum of squares for the base model (or simple mean model) used for comparison with all other models.

– For the linear regression, the sum of squared distances from each point to the line of fit reduces from 12,012.733. This is the residual or unexplained (Error) SS after fitting the model. The residual SS for a second degree polynomial fit is 6,906.997, accounting for slightly more variation than the linear fit. That is, the model accounts for more variation because the model SS are higher for the second degree polynomial than the linear fit. The C. total SS less the Error SS gives the sum of squares attributed to the model.

Mean Square

The sum of squares divided by its associated degrees of freedom. The F-ratio for a statistical test is the ratio of the following mean squares:

– The Model mean square for the linear fit is 45,265.4. This value estimates the error variance, but only under the hypothesis that the model parameters are zero.

– The Error mean square is 245.2. This value estimates the error variance.

F Ratio

The model mean square divided by the error mean square. The underlying hypothesis of the fit is that all the regression parameters (except the intercept) are zero. If this hypothesis is true, then both the mean square for error and the mean square for model estimate the error variance, and their ratio has an F-distribution.

Prob > F

The observed significance probability (p-value) of obtaining a greater F-value if the specified model fits no better than the overall response mean. Observed significance probabilities of 0.05 or less are often considered evidence of a regression effect.

Parameter Estimates Report

The terms in the Parameter Estimates report for a linear fit are the intercept and the single x variable.

For a polynomial fit of order k, there is an estimate for the model intercept and a parameter estimate for each of the k powers of the X variable.

Figure 5.13 Examples of Parameter Estimates Reports for Linear and Polynomial Fits 

The Parameter Estimates report contains the following columns:

Term

Lists the name of each parameter in the requested model. The intercept is a constant term in all models.

Estimate

Lists the parameter estimates of the linear model. The prediction formula is the linear combination of these estimates with the values of their corresponding variables.

Std Error

Lists the estimates of the standard errors of the parameter estimates. They are used in constructing tests and confidence intervals.

t Ratio

Lists the test statistics for the hypothesis that each parameter is zero. It is the ratio of the parameter estimate to its standard error. If the hypothesis is true, then this statistic has a Student’s t-distribution.

Prob>|t|

Lists the observed significance probability calculated from each t-ratio. It is the probability of getting a t-ratio greater (in absolute value) than the computed value, given a true null hypothesis. Often, a value below 0.05 (or sometimes 0.01) is interpreted as evidence that the parameter is significantly different from zero.

To reveal additional statistics, right-click in the report and select the Columns menu. The following statistics are not shown by default:

Lower 95%

The lower endpoint of the 95% confidence interval for the parameter estimate.

Upper 95%

The upper endpoint of the 95% confidence interval for the parameter estimate.

Std Beta

The standardized parameter estimate. It is useful for comparing the effect of X variables that are measured on different scales. See Parameter Estimates Report.

VIF

The variance inflation factor.

Design Std Error

The design standard error for the parameter estimate. See Parameter Estimates Report.