Multiple Comparisons
Use this option to obtain tests and confidence levels that compare means defined by levels of your model effects. The goal of multiple comparisons methods is to determine whether group means differ, while controlling the probability of reaching an incorrect conclusion. The Multiple Comparisons option lets you compare group means with the overall average (Analysis of Means) and with a control group mean. You can also conduct pairwise comparisons using either Tukey HSD or Student’s t. When you specify the Student’s t method, you can also perform equivalence tests to identify pairwise differences that are of practical importance.
The Student’s t method controls only the error rate for an individual comparison. As such, it is not a true multiple comparison procedure. All other methods provided control the overall error rate for all comparisons of interest. Each of these methods uses a multiple comparison adjustment in calculating p-values and confidence limits.
If your model contains nominal and ordinal effects, you can conduct comparisons using Least Squares Means estimates, or you can define specific comparisons using User-Defined Estimates. If your model contains only continuous effects, you can compare means using User-Defined Estimates.
Tip: Suppose that a continuous effect consists of relatively few levels. If you are interested in comparisons using Least Squares Means Estimates, consider assigning that effect an ordinal (or nominal) modeling type.
Launch the Option
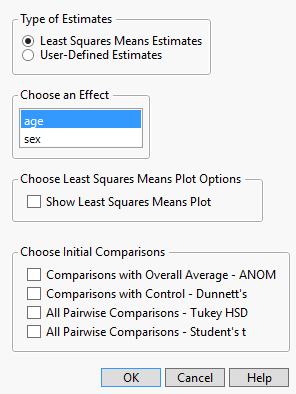
An example of the control window for the Multiple Comparisons option is shown in Figure 3.28. This example is based on the Big Class.jmp data table, with weight as Y and age, sex, and height as model effects. Two classes of estimates are available for comparisons: Least Squares Means Estimates and User-Defined Estimates.
Least Squares Means Estimates
This option compares least squares means and is available only if there are nominal or ordinal effects in the model. Recall that least squares means are means computed at some neutral value of the other effects in the model. (For a definition of least squares means, see LSMeans Table.) You must select the effect of interest. In Figure 3.28, Least Squares Means Estimates for age are specified. There is an option to show the least squares means plot. See Least Squares Means Plot Options.
Figure 3.28 Launch Window for Least Squares Means Estimates
User-Defined Estimates
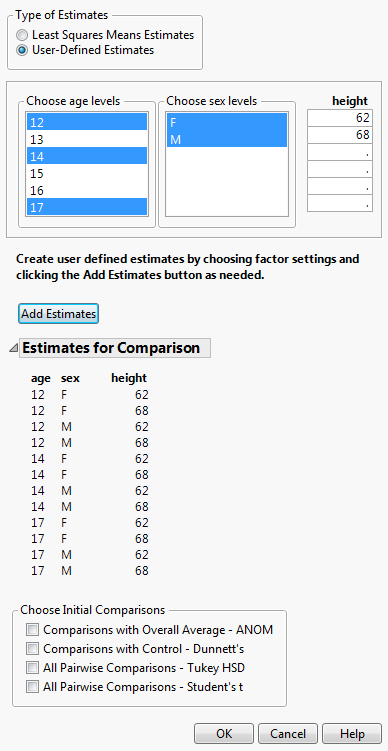
The specification of User-Defined Estimates is illustrated in Figure 3.29. Three levels of age and both levels of sex have been selected. Also, two values of height have been manually entered. The Add Estimates button has been clicked, resulting in the listing of all possible combinations of the specified levels. At this point, you can specify more estimates and click the Estimates button again to add them to the list of Estimates for Comparison.
Figure 3.29 Launch Window for User-Defined Estimates
When you use User-Defined Estimates, effects with no specified levels are set according to the modeling type:
• Continuous effects are set to the mean of the effect.
• Nominal and ordinal effects are set to the first level in the value ordering.
Note: In this section, we use the term mean to refer to either estimates of least squares means or user-defined estimates.
Choose Least Squares Means Plot Options
Select Show Least Squares Means Plot to obtain a least square means plot. If your effect is an interaction term, then you have the option to create an interaction plot. You select the term for the overlay. If you do not select the interaction plot, then the least squares plot will nest the effect terms. See Least Squares Means Plot Options.
Choose Initial Comparisons
Once you have specified estimates, you can choose the types of comparisons that you would like to see in your initial report by making selections under Choose Initial Comparisons. Or click OK without making any selections.
Comparisons with Overall Average - ANOM
Compares each effect least squares mean with the overall least squares mean. (Analysis of Means).
Comparisons with Control - Dunnett’s
Compares each effect least squares mean with the least squares mean of a control level.
All Pairwise Comparisons - Tukey HSD
Tests all pairwise comparisons of the effect least squares means using the Tukey HSD adjustment for multiplicity.
All Pairwise Comparisons - Student’s t
Tests all pairwise comparisons of the effect least squares means with no multiplicity adjustment.
Each of these selections opens a report with an area at the top that shows details specific to the report. This information includes the quantile, or critical value. For the true multiple comparisons procedures, the method used for the multiple comparison adjustment is shown. If you have specified User-Defined Estimates, the report displays a list of effects that do not vary relative to the specified estimates and the levels at which these effects are set. Unless you have specified otherwise, any continuous effect is set to its mean. Any nominal or ordinal effect is set to the first level in its value ordering.
If you click OK without selecting from the Choose Initial Comparisons list, the Multiple Comparisons report opens, showing the Least Squares Means Estimates table or the User-Defined Estimates table. From the Multiple Comparison red triangle menu, all of the options listed above are available. The available reports and options are described below.
Least Squares Means or User-Defined Estimates Report
By default, the Multiple Comparisons option displays a Least Squares Means Estimates report or a User-Defined Estimates report, depending on the type of estimates that you selected in the launch window. For each combination of levels of interest, this table gives an estimate of the mean, as well as a test and confidence interval. Specifically, this table contains the following:
Levels of the Categorical Effects
The first columns in the report identify the effect or effects of interest. The values in the columns specify the groups being analyzed.
Estimate
An estimate of the mean for each group.
Std Error
The standard error of the mean for each group.
DF
The degrees of freedom for a test of whether the mean is 0.
Lower 95%
The lower confidence limit for the mean. You can change the confidence level by selecting Set Alpha Level in the Fit Model window.
Upper 95%
The upper confidence limit for the mean.
t Ratio
The t ratio for the significance test. This column appears only if you right-click in the report and select Columns > t Ratio.
Prob>|t|
The p-value for the significance test. This column appears only if you right-click in the report and select Columns > Prob>|t|.
Arithmetic Mean Estimate
(Appears only in the Least Squares Means Estimates report.) An estimate of the arithmetic mean for each group.
N
(Appears only in the Least Squares Means Estimates report.) The number of observations used to calculate the mean for each group.
Note: You can obtain t ratios and p-values by right-clicking in the table and selecting Columns.
Comparisons with Overall Average
This option compares the means for the specified levels specified to the overall mean for these levels. It displays a table showing confidence intervals for differences from the overall mean and a chart showing decision limits. The method used to make the comparisons is called analysis of means (ANOM) (Nelson et al. 2005). ANOM is a multiple comparison procedure that controls the joint error rate for all pairwise comparisons to the overall mean. See Figure 3.30 for a report based on the Lipid Data.jmp sample data table.
ANOM might appear similar to analysis of variance. However, it is fundamentally different in that it identifies levels with means that differ from the overall mean for all levels. In contrast, analysis of variance tests for differences in the means themselves.
At the top of the Comparisons with Overall Average report, you find:
Quantile
The value of Nelson’s h statistic used in constructing the decision limits.
Adjusted DF
The degrees of freedom used in constructing the decision limits.
Avg
The average mean. For least squares estimates, the average mean is a weighted average of the group least squares means. This weighted average represents the overall mean at the neutral settings where the group least squares means are calculated.
Specifically, the average least squares mean is a weighted average with weights inversely proportional to the diagonal entries of the matrix L(X′X)−1L′. Here L is the matrix of coefficients used to compute the group least squares means. For a technical definition of least squares means, see the GLM Procedure chapter in SAS Institute Inc. (2020b).
For user-defined estimates, the average mean is defined similarly. However, in this case, L is the matrix of coefficients used to define the estimates.
Adjustment
Describes the method used to obtain the critical value:
Nelson
Provides exact critical values and p-values. Used whenever possible, in particular, when the estimates are uncorrelated.
Nelson-Hsu
Provides approximate critical values and p-values based on Hsu’s factor analytical approximation is used (Hsu 1992). Used when exact values cannot be obtained.
Sidak
Used when both Nelson and Nelson-Hsu fail.
For technical details, see the GLM Procedure chapter in SAS Institute Inc. (2020b).
Three options are available from the Comparisons with Overall Average report menu:
Differences from Overall Average
For each comparison of a group’s mean to the overall mean, this report provides the following details:
• The levels being compared
• Difference - the estimated difference
• Std Error - the standard error of the difference
• Lower and Upper limits for the confidence interval
• t Ratio - the ratio of the Difference and Std Error columns
Comparisons with Overall Average Decision Chart
This decision chart plots a point at the mean for each group. A horizontal line is plotted at the average mean. Upper and lower decision limits are plotted. Suppose that a point corresponding to a group mean falls outside these limits. This occurrence indicates that the group mean differs from the overall mean, based on the analysis of means test at the specified significance level. The significance level is shown below the chart.
The Comparisons with Overall Average Decision Chart report menu has these options:
Show Summary Report
Produces a table showing the estimate, decision limits, and the limit exceeded for each group
Display Options
Gives several options for controlling the display of the chart.
Calculate Adjusted P-Values
Adds a column that contains p-values (Prob>|t|) to the Comparisons with Overall Average report. Note that computing exact critical values and p-values for unbalanced designs requires complex integration and can be computationally challenging. When calculations for such a quantile fail, the Sidak quantile is computed but p-values are not available.
Example of Comparisons with Overall Average
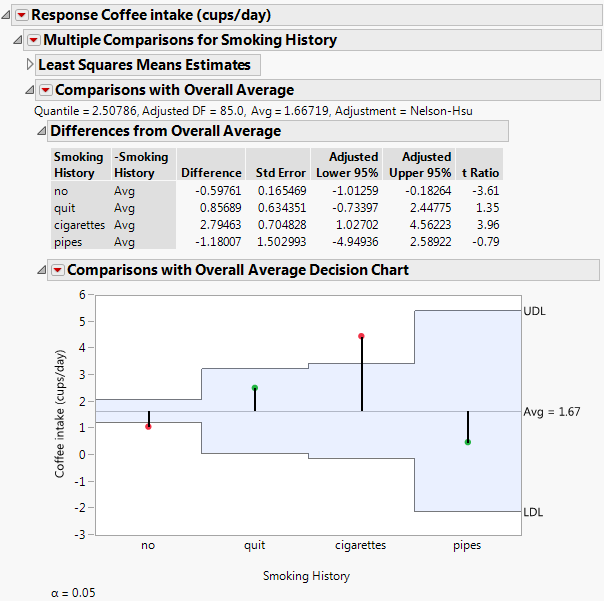
Consider the Lipid Data.jmp sample data table. You are interested in whether any of the four Smoking History categories are unusual in that their mean Coffee intake (cups/day) differ from the overall average coffee intake while controlling for alcohol use and heart history. You specify a model with Coffee intake (cups/day) as the response and Smoking History, Alcohol Use, and Heart History as model effects.
1. Select Help > Sample Data Library and open Lipid Data.jmp.
2. Select Analyze > Fit Model.
3. Select Coffee intake (cups/day) and click Y.
4. Select Smoking History, Alcohol Use, and Heart History, and click Add.
5. Click Run.
6. Click the red triangle next to Response Coffee intake (cups/day) and select Estimates > Multiple Comparisons.
7. From the Choose an Effect list, select Smoking History.
8. In the Choose Initial Comparisons list, select Comparisons with Overall Average - ANOM.
9. Click OK.
The results shown in Figure 3.30 indicate that the least squares means for non-smokers and cigarette smokers differ significantly from the overall average in terms of coffee intake.
Figure 3.30 Comparisons with Overall Average for Ratings
Comparisons with Control
If you select Comparisons with Control - Dunnett’s, a window opens, asking you to specify a control group. If you selected Least Squares Means Estimates, the list consists of all levels of the effect you that you selected. If you selected User-Defined Estimates, the list consists of the combinations of effect levels that you specified.
After you choose a control group and click OK, the Comparisons with Control report appears in your Fit Least Squares report. This option compares the means for the specified settings to the control group mean. It displays a table showing confidence intervals for differences from the control group and a chart showing decision limits. Dunnett’s method is used to make the comparisons. Dunnett’s method is a multiple comparison procedure that controls the error rate over all comparisons (Hsu 1996; Westfall et al. 2011).
When exact calculation of p-values and confidence intervals is not possible, Hsu’s factor analytical approximation is used (Hsu 1992). Note that computing exact critical values and p-values for unbalanced designs requires complex integration and can be computationally intensive. When calculations for such a quantile fail, the Sidak quantile is computed.
In addition to the list of effects that do not vary for the specified estimates, at the top of the Comparisons with Control report you also find:
Quantile
The critical value for Dunnett’s test.
Adjusted DF
The degrees of freedom used in constructing the confidence intervals.
Control
The setting that defines the control group. This is a single level if you have selected a single effect; it is a combination of levels if you specified a user-defined combination of more than one effect.
Adjustment
The method used to obtain the critical value:
Dunnett
Provides exact critical values and p-values. Used whenever possible, in particular, when the estimates are uncorrelated.
Dunnett-Hsu
Provides approximate critical values and p-values based on Hsu’s factor analytical approximation (Hsu 1992). Used when exact values cannot be obtained.
Sidak
Used when both Dunnett and Dunnett-Hsu fail.
For technical details, see the GLM Procedure chapter in SAS Institute Inc. (2020b).
Three options are available from the Comparisons with Control report menu:
Differences from Control
For each comparison of a group mean to the control mean, this report provides the following details:
• The levels being compared
• Difference - the estimated difference
• Std Error - the standard error of the difference
• Lower and Upper limits for the confidence interval
• t Ratio - the ratio of the Difference and Std Error columns
Comparisons with Control Decision Chart
This decision chart plots a point at the mean for each group being compared to the control group. A horizontal line shows the mean for the control group. Upper and lower decision limits are plotted. When a point falls outside these limits, it corresponds to a group whose mean differs from the control group mean based on Dunnett’s test at the specified significance level. That level is shown beneath the chart.
The Comparisons with Control Decision Chart report menu has these options:
Show Summary Report
Produces a table showing the estimate, decision limits, and the limit exceeded for each group
Display Options
Gives several options for controlling the display of the chart.
Calculate Adjusted P-Values
Adds a column that contains p-values (Prob>|t|) to the Comparisons with Control report. Note that computing exact critical values and p-values for unbalanced designs requires complex integration and can be computationally challenging. When calculations for such a quantile fail, the Sidak quantile is computed but p-values are not available.
All Pairwise Comparisons
The All Pairwise Comparisons option shows either a Tukey HSD All Pairwise Comparisons or Student’s t All Pairwise Comparisons report (Hsu 1996; Westfall et al. 2011). Tukey HSD comparisons are constructed so that the significance level applies jointly to all pairwise comparisons. In contrast, for Student’s t comparisons, the significance level applies to each individual comparison. When making several pairwise comparisons using Student’s t tests, the risk that one of the comparisons incorrectly signals a difference can well exceed the stated significance level.
At the top of the Tukey HSD All Pairwise Comparisons report you find:
Quantile
The critical value for the test. Note that, for Tukey HSD, the quantile is 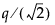 , where q is the appropriate percentage point of the Studentized range statistic.
, where q is the appropriate percentage point of the Studentized range statistic.
Adjusted DF
The degrees of freedom used in constructing the confidence intervals.
Adjustment
Describes the method used to obtain the critical value:
Tukey
Provides exact critical values and p-values. Used when the means are uncorrelated and have equal variances, or when the design is variance-balanced.
Tukey-Kramer
Provides approximate critical values and p-values. Used when exact values cannot be obtained.
For technical details, see the GLM Procedure chapter in SAS Institute Inc. (2020b).
At the top of the Student’s t All Pairwise Comparisons report you find the Quantile, or critical value, for the t test and DF, the degrees of freedom used for the t test.
All Pairwise Differences Report
Both Tukey HSD and Student’s t compare all pairs of levels. For each pairwise comparison, the All Pairwise Differences report shows:
• The levels being compared
• Difference - the estimated difference between the means
• Std Error - the standard error of the difference
• t Ratio - the t ratio for the test of whether the difference is zero
• Prob > |t| - the p-value for the test
• Lower and Upper limits for a confidence interval for the difference in means
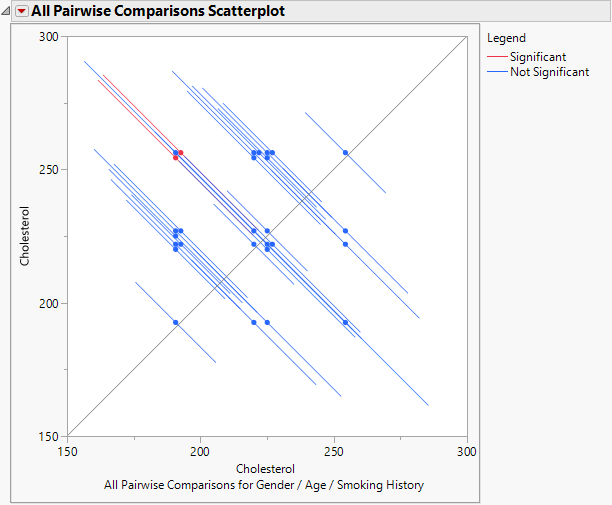
All Pairwise Comparisons Scatterplot
This plot, sometimes called a diffogram or a mean-mean scatterplot, displays the confidence intervals for all means pairwise differences. (See Figure 3.32 for an example.) Colors indicate which differences are significant.
The plot shows a reference line as an upwardly sloping line on the diagonal. This line represents points where the two means are equal. Each line segment corresponds to a confidence interval for a pairwise comparison. The coordinates of the point displayed on the line segment are the means for the corresponding groups. Hover over one of these points to show a tooltip that identifies the groups being compared and shows the estimated difference. If a line segment crosses the line on the diagonal, then the means can be equal and the comparison is not significant.
The Pairwise Comparisons Scatterplot has the following option:
Show Reference Lines
Displays reference grid lines for the points on the scatterplot. This is not recommended if there are many points in the scatterplot. If there are many points, it is better to hover over the points to view the tooltip labels.
All Pairwise Differences Connecting Letters
Use this option to display a report that illustrates significant and non-significant comparisons with connecting letters. Levels not connected by the same letter are significantly different. Levels connected by the same letter are not significantly different.
Save All Pairwise Differences Connecting Letters Table
This option creates a data table whose columns contain the levels of the effect, the connecting letters, the least squares means, their standard errors, and confidence intervals. The data table contains a script called Bar Chart that produces a colored bar chart of the least squares means with their confidence intervals superimposed. The levels are arranged in decreasing order of least squares means.
Equivalence Tests
Use this option to conduct one or more equivalence tests. Equivalence tests are useful when you want to detect differences that are of practical interest. You must specify a threshold difference for group means for which smaller differences are considered practically equivalent. In other words, if two group means differ by this amount or less, you are willing to consider them equivalent.
Once you have specified this value, the Equivalence Tests report appears. The bounds that you have specified are given at the top of the report. The report consists of a table giving the equivalence tests and a scatterplot that displays them. The equivalence tests and confidence intervals are based on Student’s t critical values.
Note: Equivalence tests are available only for the Student’s t method.
Equivalence TOST Tests
The Two One-Sided Tests (TOST) method is used to test for a practical difference between the means (Schuirmann 1987). Two one-sided pooled-variance t tests are constructed for the null hypotheses that the true difference exceeds the threshold values. If both tests reject, the difference in the means does not statistically exceed either threshold value. Therefore, the groups are considered practically equivalent. If only one or neither test rejects, then the groups might not be practically equivalent.
For each comparison, the Equivalence TOST Tests report gives the following information:
• Difference - the estimated difference in the means
• Lower Bound t Ratio, Upper Bound t Ratio - the lower and upper bound t ratios for the two one-sided pooled-variance significance tests
• Lower Bound p-Value, Upper Bound p-Value - p-values corresponding to the lower and upper bound t ratios
• Maximum p-Value - the maximum of the lower and upper bound p-values
• Lower and Upper limits for a 1−2α confidence interval for the difference in the means.
Note: Equivalence TOST tests are available only for the Student’s t method.
Equivalence Tests Scatterplot
Using colors, this scatterplot indicates which means are practically equivalent and which are not practically equivalent as determined by the equivalence test. This plot is sometimes called a diffogram or a mean-mean scatterplot.
The plot shows a solid reference line on the diagonal as well as a shaded reference band. The width of the band is twice the practical difference. The coordinates of the point on the line segment are the means for the corresponding groups. There is an implied third axis on the diagonal where each line segment corresponds to a 1−2α confidence interval for a pairwise comparison. Hover over one of these points to show a tooltip that indicates the groups being compared and the estimated difference. When a line segment is entirely contained within the diagonal band, it follows that the means are practically equivalent.
Note: Equivalence tests scatterplots are available only for the Student’s t method.
The Equivalence Tests Scatterplot has the following option:
Show Reference Lines
Displays reference lines for the points on the scatterplot. This is not recommended if there are many points in the scatterplot. If there are many points, it is better to hover over the points to view the tooltip labels.
Remove
This option removes the Equivalence Tests report from the Student’s t All Pairwise Comparisons report.
Example of Tukey HSD All Pairwise Comparisons
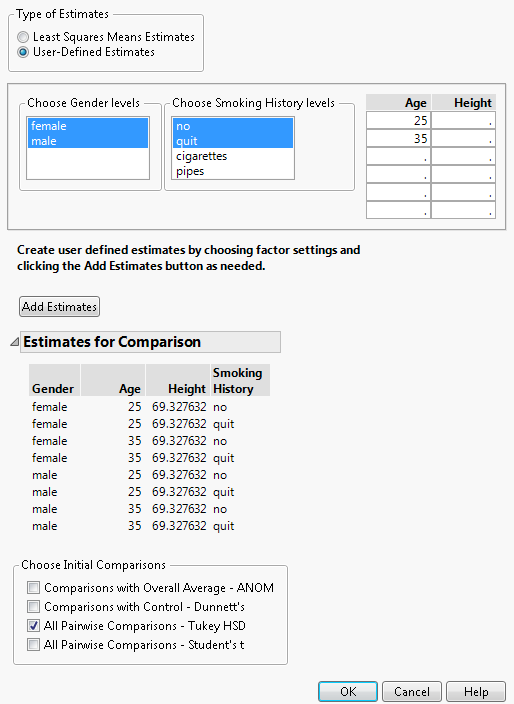
Consider the Lipid Data.jmp sample data table. You are interested in Cholesterol differences for gender and non-smokers versus former smokers (Smoking History equal to no and quit, respectively) across two ages (25 and 35) and average height.
1. Select Help > Sample Data Library and open Lipid Data.jmp.
2. Select Analyze > Fit Model.
3. Select Cholesterol and click Y.
4. Select Gender, Age, Height, and Smoking History, and click Add.
5. Click Run.
6. Click the red triangle next to Response Cholesterol and select Estimates > Multiple Comparisons.
7. From the Type of Estimates list, click User-Defined Estimates.
8. From the Choose Gender levels list, select female (it should already be selected by default) and male.
9. From the Choose Smoking History levels list, select no and quit.
10. In the Age list, enter the ages 25 and 35 in the first two rows.
Do not enter any values in the list entitled Height. Because no values for Height are specified, the mean value of the Height column is used in the multiple comparisons report.
11. Click Add Estimates.
Note that all possible combinations of the levels that you specified appear in the Estimates for Comparison report.
12. In the Choose Initial Comparisons list, select All Pairwise Comparisons - Tukey HSD.
Check that your window is completed as shown in Figure 3.31.
Figure 3.31 Populated Used-Defined Estimates Window
13. Click OK.
The All Pairwise Differences report indicates that two of the 28 pairwise comparisons are significant. The All Pairwise Comparisons Scatterplot, shown in Figure 3.32, shows the confidence intervals for these comparisons in red. You can hover over any of the points to determine which pairwise comparison the point represents. The tooltips also contain the difference between the two levels in the comparison. The two red points in Figure 3.32 represent the points comparing 35-year-old former smokers to 25-year-old non-smokers, for both females and males.
Figure 3.32 All Pairwise Comparisons Scatterplot for User-Defined Comparisons