Options for Model Effects
The menu icon beside each effect name gives you the following options to request additional information about the multivariate fit:
Test Details
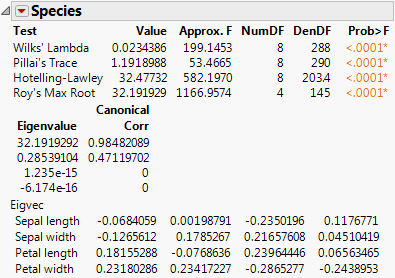
Displays the eigenvalues and eigenvectors of the E−1H matrix used to construct multivariate test statistics. See Test Details.
Centroid Plot
Plots the centroids (multivariate least squares means) on the first two canonical variables formed from the test space. See Centroid Plot.
Save Canonical Scores
Saves variables called Canon[1], Canon[2], and so on, as columns in the current data table. These columns have both the values and their formulas. For an example, see Save Canonical Scores. For technical details, see Canonical Details.
Contrast
Performs the statistical contrasts of treatment levels that you specify in the contrasts dialog.
Note: The Contrast command is the same as for regression with a single response. See the LSMeans Contrast, for a description and examples of the LSMeans Contrast commands.
Test Details
The Test Details report gives canonical details about the test for the whole model or the specified effect.
Eigenvalue
The eigenvalues of the E−1H matrix used in computing the multivariate test statistics.
Canonical Corr
The canonical correlations associated with each eigenvalue. This is the canonical correlation of the transformed responses with the effects, corrected for all other effects in the model.
Eigvec
The eigenvectors of the E−1H matrix, or equivalently of (E + H)−1H.
Example of Test Details
1. Select Help > Sample Data Library and open Iris.jmp.
The Iris data (Mardia et al. 1979) have three levels of Species named Virginica, Setosa, and Versicolor. There are four measures (Petal length, Petal width, Sepal length, and Sepal width) taken on each sample.
2. Select Analyze > Fit Model.
3. Select Petal length, Petal width, Sepal length, and Sepal width and click Y.
4. Select Species and click Add.
5. For Personality, select Manova.
6. Click Run.
7. Click the Choose Response button and select Identity.
8. Click Run.
9. Click the Species red triangle and select Test Details.
The eigenvalues, eigenvectors, and canonical correlations appear.
Figure 9.5 Test Details
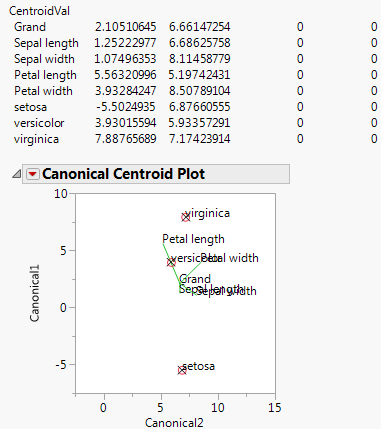
Centroid Plot
The Centroid Plot command (accessed from the Species red triangle) plots the centroids (multivariate least squares means) on the first two canonical variables formed from the test space, as in Figure 9.6. The first canonical axis is the vertical axis so that if the test space is only one dimensional the centroids align on a vertical axis. The centroid points appear with a circle corresponding to the 95% confidence region (Mardia et al. 1979). When centroid plots are created under effect tests, circles corresponding to the effect being tested appear in red. Other circles appear blue. Biplot rays show the directions of the original response variables in the test space. See Details for Centroid Plot Option.
Click the Centroid Val disclosure icon to show additional information, shown in Figure 9.6.
The first canonical axis with an eigenvalue accounts for much more separation than does the second axis. The means are well separated (discriminated), with the first group farther apart than the other two. The first canonical variable seems to load the petal length variables against the petal width variables. Relationships among groups of variables can be verified with Biplot Rays and the associated eigenvectors.
Figure 9.6 Centroid Plot and Centroid Values
Save Canonical Scores
Saves columns called Canon[i] to the data table, where i refers to the ith canonical score for the Y variables. The canonical scores are computed based on the E−1H matrix used to construct the multivariate test statistic. Canonical scores are saved for eigenvectors corresponding to nonzero eigenvalues.
Canonical Correlation
Canonical correlation analysis is not a specific command, but it can be performed using a sequence of commands in the multivariate fitting platform.
1. Follow step 1 through step 8 in Example of Test Details.
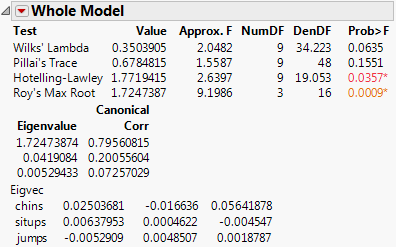
2. Click the Whole Model red triangle and select Test Details.
3. Click the Whole Model red triangle and select Save Canonical Scores.
The details list the canonical correlations (Canonical Corr) next to the eigenvalues. The saved variables are called Canon[1], Canon[2], and so on. These columns contain both the values and their formulas.
To obtain the canonical variables for the X side, repeat the same steps, but interchange the X and Y variables. If you already have the columns Canon[n] appended to the data table, the new columns are called Canon[n] 2 (or another number) that makes the name unique.
This is an additional example of canonical correlation analysis.
1. Select Help > Sample Data Library and open Exercise.jmp.
2. Select Analyze > Fit Model.
3. Select chins, situps, and jumps and click Y.
4. Select weight, waist, and pulse and click Add.
5. For Personality, select Manova.
6. Click Run.
7. Click the Choose Response button and select Identity.
8. Click Run.
9. Click the Whole Model red triangle and select Test Details.
10. Click the Whole Model red triangle and select Save Canonical Scores.
Figure 9.7 Canonical Correlations
The output canonical variables use the eigenvectors shown as the linear combination of the Y variables. For example, Canon[1] is calculated as follows:
0.02503681*chins + 0.00637953*situps + -0.0052909*jumps
This canonical analysis does not produce a standardized variable with mean 0 and standard deviation 1, but it is easy to define a new standardized variable with the calculator that has these features.