The Process Screening Report
The Process Screening report opens with a Summary table that contains results about process stability. There is a label above the summary table that shows the type of control chart on which the results are based. The sample size or subgroup variable is also shown above the summary table for every chart type except for Indiv and MR. The summary table also contains capability results if you have provided specification limits. The processes and groups are initially sorted in decreasing order by Stability Index. If Importance values are specified by the user, the processes and groups are sorted in decreasing order by Stability Index within Importance. The columns for Stability Index, Ppk, Cpk, Cp, and Target Index are colored as green, yellow, and red to indicate adequate, marginal, and poor stability or capability, respectively. This color coding scheme matches the Process Performance graph color coding scheme.
Tip: To sort the report by a column, click the column name. A caret appears to the right of the column name. The direction of the caret indicates whether the sorting is descending or ascending. To change the order of the sorting, click the column name again.
The control chart calculations in the Summary table include Nelson tests and a Range Limit Exceeded test. These tests assume the following about the control chart limits:
• The center line for the XBar or X control charts is given by the mean of all measurements. If you use the Medians instead of Means option, the center line is given by the median of the observations.
• Control limits are placed at K sigma units from the center line. Use the KSigma option in the launch window to specify K. By default, KSigma is 3.
• Sigma is estimated using the conventions that correspond to the control chart type that you specified or, if you use Medians instead of Means, as described in Use Medians instead of Means.
Tip: The eight Nelson tests in the Process Screening platform follow the test settings in the Control Chart Builder platform preferences. You can customize the tests at File > Preferences > Platforms > Control Chart Builder.
The Summary table can contain the following information:
Column
The columns that you entered as Process. There is a row for each distinct combination of Process and Grouping columns. This column is suppressed if there is only one process column.
Tip: To access options that operate on selected items, right-click the Column column.
Grouping Columns
There is a report column for each column in the data table that you entered as Grouping. The levels of the Grouping columns are listed so that there is a unique row in the report table for each distinct combination of Process name and Grouping columns values.
Importance
(Appears only when there are importance values specified by the user, as inputs from a limits table.) The user-specified importance value for the processes.
Variability
Contains the following columns:
Stability Index
A measure of stability of the process. A stable process has a stability index near one. Higher values indicate less stability. The stability index is defined as follows:
(Overall Sigma / Within Sigma)
If a three way control chart is selected in the launch, the stability index is defined as follows:
(Overall Sigma / Between-and-Within Sigma)
Stability Ratio
A measure of stability of the process. A stable process has a stability ratio near one. Higher values indicate less stability. The stability ratio is defined as follows:
(Overall Sigma / Within Sigma)2
If a three way control chart is selected in the launch, the stability ratio is defined as follows:
(Overall Sigma / Between-and-Within Sigma)2
Within Sigma
An estimate of the standard deviation based on within subgroup variation. The estimate is based on the control chart type that you specified, and is a short-term measure of variation. See Statistical Details for the Process Capability Platform in Quality and Process Methods for statistical details. If you select Medians instead of Means, Within Sigma is computed as described in Use Medians instead of Means.
Overall Sigma
The usual estimate of standard deviation based on all observations.
Between Sigma
(Appears only when three way control chart is selected in the launch window.) An estimate of the standard deviation based on the variation between subgroups. See Statistical Details for the Process Capability Platform in Quality and Process Methods for statistical details.
Between-and-Within Sigma
(Appears only when three way control chart is selected in the launch window.) An estimate of the standard deviation based on the variation between subgroups and the variation within subgroups. The Between-and-Within Sigma estimate is defined as follows:
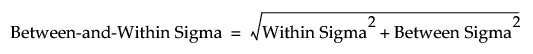
Specified Sigma
The standard deviation specified by a sigma control limit in the Limits Specification dialog or an estimate of the standard deviation derived from the control limits and subgroup size. See Derived Sigma. The control limits and subgroup size can be specified using a limits table or a Control Limits column property.
Summary
Contains the following columns:
Centerline
(Appears if you do one of the following: select Use Medians instead of Means in the launch window, import a Center value using a limits table, or import control limits to derive sigma.) The value listed under Centerline is used in control chart calculations as the center line.
– If you select Use Medians instead of Means in the launch window, the overall median of the observations is displayed.
– If you import a Center value from a limits table, that value is displayed.
– If you import control limits, the value displayed is calculated as (UCL + LCL)/2.
Mean
The average of all observations.
Count
The number of observations.
N Subgroups
The number of subgroups.
Control Chart Alarms
Contains information about the subgroups that result in alarms for a variety of tests, including each of the 8 Western Electric rules. The standard deviation estimate is the Within Sigma value. By default, only the Alarm Rate, Test 1, and Latest Alarm columns are shown in the Summary table.
Alarm Rate
The number of subgroups that resulted in alarms for any of the tests selected under the Choose Test option (Any Alarm) divided by the number of non-missing subgroups (Subgroups).
Any Alarm
(Appears only when more than one Test column is shown.) The number of subgroups that trigger alarms for any of the tests selected under the Choose Test option. These are the eight Nelson tests and the test for Range Limit Exceeded.
Tip: The eight Nelson tests in the Process Screening platform follow the test settings in the Control Chart Builder platform preferences. You can customize the tests at File > Preferences > Platforms > Control Chart Builder.
Test 1
One point is more than three standard deviations from the center line. The subgroup associated with that point triggers the alarm.
Test 2
Nine or more consecutive points are on the same side of the center line. The subgroup associated with the ninth point triggers the alarm.
Test 3
Six or more consecutive points are continually increasing or decreasing. The subgroup associated with the sixth point triggers the alarm.
Test 4
Fourteen consecutive points alternate in direction: increasing and then decreasing or decreasing and then increasing. The subgroup associated with the 14th point triggers the alarm.
Test 5
Two out of three consecutive points on the same side of the center line are more than two standard deviations from the center line. The subgroup associated with the second point that exceeds two standard deviations triggers the alarm.
Test 6
Four out of five consecutive points on the same side of the center line are more than one standard deviation from the center line. The subgroup associated with the fourth point that exceeds one standard deviation triggers the alarm.
Test 7
Fifteen consecutive points, on either side of the center line, are all within one standard deviation of the center line. The subgroup associated with the 15th point triggers the alarm.
Test 8
Eight consecutive points, on either side of the center line, all fall beyond one standard deviation of the center line. The subgroup associated with the eighth point triggers the alarm.
Range Limit Exceeded
The number of subgroups that exceed the upper control limit on the R, S, or MR chart calculation.
Moving Range Limit Exceeded
The number of subgroups that exceed the moving range limit on the three way control chart calculation.
Latest Alarm
The position of the subgroup, counting from the last subgroup, that signaled the most recent alarm for any of the Nelson or Range Limit Exceeded tests.
Capability
(Appears only when there are Spec Limits specified for some processes.) Contains the following options:
Ppk
Capability index based on Overall Sigma and assuming a normal distribution. See Statistical Details for the Process Capability Platform in Quality and Process Methods for statistical details. On by default.
Cpk
Capability index based on Within Sigma or Between-and-Within Sigma and assuming a normal distribution. See Statistical Details for the Process Capability Platform in Quality and Process Methods for statistical details. On by default.
Cp
The potential capability if target and drift issues are resolved. See Capability Indices for Normal Distributions in Quality and Process Methods for details.
Target Index
The number of short-term standard deviations that the process average differs from the target value. This measures the ability of the process to hit the target value. The Target Index is calculated as 3(Cp - Cpk). A target index is considered poor if above 1, marginal if between 0.5 and 1, and adequate if less than 0.5. See White et al. (2018).
Out of Spec Count
The number of observations that fall outside the specification limits. On by default.
Out of Spec Rate
The proportion of observations that fall outside the specification limits. On by default.
Expected Out of Spec Rate
The expected proportion of observations that fall outside of the specification limits. The Expected Out of Spec Rate assumes a stable and normally distributed process and uses overall sigma.
Latest Out of Spec
The number of observations, counting from the last observation to the most recent observation that falls outside the specification limits. On by default.
(Mean-Tgt)/SpecRange
The spec centered mean. This is the same as the Mean Shift Standardized to Spec in Process Capability. See Goal Plot in Quality and Process Methods for statistical details.
StdDev/SpecRange
The spec scaled standard deviation. This is the same as the Std Deviation Standardized to Spec in Process Capability. See Goal Plot in Quality and Process Methods for statistical details.
LSL
The lower specification limits.
USL
The upper specification limits.
Target
The target value.
Shift Magnitudes and Positions
(Shown only if you have selected a Shift Detection option from the Process Screening red triangle menu.) Shift detection is performed to identify shifts that exceed one within-sigma unit. The algorithm uses outlier-correction and an EWMA smoothing approach for the individual observations. This is the algorithm:
– Outliers are removed so that single outliers do not indicate shifts. The value specified as Outlier Threshold (five by default) on the launch window controls the sensitivity of outlier removal. If the number of within-sigma units from an observation to both of its neighboring observations exceeds the specified Outlier Threshold, that observation is replaced with a value that is one within-sigma unit away from its closest neighboring observation.
– An EWMA fit is constructed for the subgroup means in forward time order and another EWMA fit is constructed for the subgroup means in reverse time order. The EWMA fits have lambda equal to 0.3.
– The largest positive and negative differences between successive EWMA values that exceed one within-sigma unit are identified.
– The absolute values of these differences, divided by the within estimate of sigma, are the values reported as Largest Upshift and Largest Downshift.
– The locations of the first subgroups involved in these largest shifts define the Upshift Position and Downshift Position.
Largest Upshift
The magnitude of the largest upward shift that exceeds one within-sigma unit, reported in within-sigma units.
Upshift Position or Upshift <Time Variable>
The position of the subgroup having the largest Upshift. If you specify a Time variable, the column in the Summary table is named Upshift <Time Variable> and the position of the shift is given in terms of the Time variable.
Largest Downshift
The magnitude of the largest downward shift that exceeds one within-sigma unit, reported in within-sigma units.
Downshift Position or Downshift <Time Variable>
The position of the subgroup having the largest Downshift. If you specify a Time variable, the column in the Summary table is named Downshift <Time Variable> and the position of the shift is given in terms of the Time variable.
Drift Magnitudes and Positions
(Shown only if you have selected the Drift Summaries option from the Process Screening red triangle menu.) Drift detection is performed to detect smaller, more gradual changes in processes. The algorithm is identical to the one used in shift detection, except that drift detection uses a Holt Double-Exponential Smoother instead of an EWMA. This is the algorithm:
– Outliers are removed through the same process that is used in shift detection. See Shift Magnitudes and Positions.
– The drift detection algorithm fits a Holt Double-Exponential Smoothing model for the subgroup means in forward time order and fits another Holt Double-Exponential Smoothing model for the subgroup means in reverse time order. The two smoothing model fits each have two smoothing constants: α for the level and β for the slope. The β smoothing constant is set at 0.05 and the α smoothing constant is estimated to minimize the error.
– The means of the positive drift values, negative drift values, and absolute drift values are reported as Mean Up Drift, Mean Down Drift, and Mean Abs Drift, respectively.
Mean Up Drift
The sum of the positive drift values divided by the count.
Mean Down Drift
The sum of the negative drift values divided by the count.
Mean Abs Drift
The sum of the absolute value of all drift values divided by the count.
Note: Process Screening does not utilize the Distribution or Process Capability Distribution column properties and always performs capability analyses assuming a normal distribution. If the distribution type for one of these column properties is non-normal, a Warnings outline is shown below the Summary table.