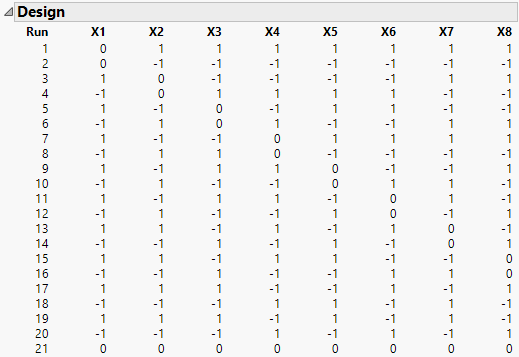
Structure of Definitive Screening Designs
Figure 7.22 shows an example of a definitive design with eight continuous factors. and four Extra Runs that correspond to fake factors. Notice the following:
• Each pair of rows is a foldover pair; each even-numbered row is -1 times the previous row. The foldover aspect of the design removes the confounding of two-factor interactions and main effects.
• Each factor is set at its center value for three runs; this, together with the design’s construction, makes all quadratic effects estimable.
• Rows 17 through 20 are the Extra Runs that correspond to the fake factors.
• Adding the center run in the last row enables you to fit a model that includes an intercept and all main and quadratic effects.
This structure is typical of definitive screening designs for continuous factors.
Figure 7.22 Definitive Screening Design for Eight Continuous Factors
Conference Matrices and the Number of Runs
Definitive screening designs in JMP are constructed using conference matrices (Xiao et al., 2012). A conference matrix is an m x m matrix C where m is even. The matrix C has 0s on the diagonal, off-diagonal entries equal to 1 or –1, and satisfies
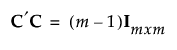 .
.
Note: For certain even values of m, it is not known if a conference matrix exists.
Suppose that the number of factors, k, is five or larger. For the case of k ≤ 4 factors, see Definitive Screening Designs for Four or Fewer Factors.
Consider the case of k continuous factors and suppose that a conference matrix is available.
• When k is even, the k x k conference matrix is used to define k runs of the design. Its negative, –C, defines the foldover runs. A center point is added to the design to ensure that a model containing an intercept, main effects, and quadratic effects is estimable. So, for k even, the minimum number of runs in the definitive screening design is 2k + 1.
• When k is odd, a (k+1) x (k+1) conference matrix is used, with its last column deleted. A center point is added. Thus, for k odd, the minimum number of runs in the screening design is 2k + 3.
A similar procedure is used when some factors are categorical and a conference matrix is available. See Jones and Nachtsheim (2013).
• Instead of a single center point, two additional runs are required. These two runs are center runs where all continuous factors are set at their middle values.
• When there are k factors and k is even, the number of runs in the design is 2k + 2.
• When k is odd, the number of runs is 2k + 4.
For those values of m for which a conference matrix is not available, a definitive screening design can be constructed using the next largest conference matrix. As a result, the required number of runs might exceed 2k + 3, in the continuous case, and 2k + 4, in the categorical case.
Extra Runs
Extra runs are constructed using fictitious, or fake, factors. Adding f fake factors to a design results in 2f additional runs.
Denote the number of factors in your experimental study by k. Four or eight extra runs can be added to a design. Extra runs are constructed by creating a design for k + f factors, as described in Conference Matrices and the Number of Runs, and then dropping the last f columns. As few as four extra runs can be highly beneficial in model selection.
For information about how extra runs are used, see Effective Model Selection for DSDs.
Definitive Screening Designs for Four or Fewer Factors
Definitive screening designs for four or fewer factors are constructed using the five-factor definitive screening design as a base. This is because designs for k ≤ 4 factors constructed strictly according to the conference matrix approach have undesirable properties. In particular, it is difficult to separate second-order effects.
If you specify k ≤ 4 factors, a definitive screening design for five factors is constructed and unnecessary columns are dropped. For this reason, the number of runs for an unblocked design with k ≤ 4 factors is 13 if all factors are continuous or 14 if some factors are categorical.