Visualizing the Latin Hypercube Design
To visualize the nature of the Latin Hypercube technique, create a plot with Graph Builder:
1. Create another Latin Hypercube design using two factors.
2. Select DOE > Special Purpose > Space Filling Design.
3. Enter two factors and be sure to change the factor values so that they are 0 and 1 instead of the default –1 and 1.
4. Click Continue.
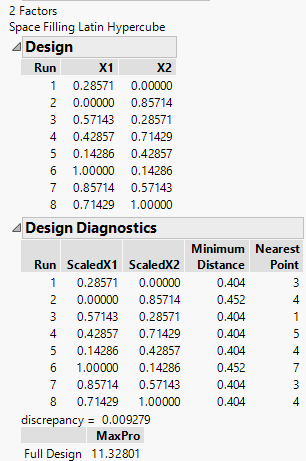
5. Specify a sample size of eight (Number of Runs).
6. Click Latin Hypercube.
Figure 21.12 Latin Hypercube Design with Two Factors and Eight Runs
7. Click Make Table.
8. Select Graph > Graph Builder.
9. Specify X1 as X and X2 as Y.
10. Click the smoother icon to remove the smoother (blue line) from your graph.
11. Right-click the plot and select Graph > Size/Scale > Size to Isometric to adjust the frame size so that the frame is square.
12. Right-click the plot, select Customize from the menu. In the Customize panel, click the large plus sign to see a text edit area, and enter the following script:
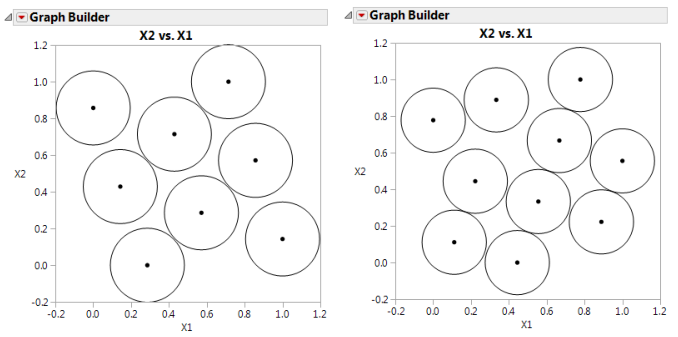
For Each Row(Circle({:X1, :X2}, 0.404/2))where 0.404 is the minimum distance number that you noted in the Design Diagnostics panel (Figure 21.12). This script draws a circle centered at each design point with radius 0.202 (half the diameter, 0.404), as shown on the left in Figure 21.13. This plot shows the efficient way JMP packs the design points.
13. Repeat the above procedure exactly, but with 10 runs instead of eight (step 5). Remember to change 0.404 in the graphics script to the minimum distance produced by 10 runs.
You should see a graph similar to the one on the right in Figure 21.13. Note the irregular nature of the sphere packing. In fact, you can repeat the process to get a slightly different picture because the arrangement is dependent on the random starting point.
Figure 21.13 Comparison of Latin Hypercube Designs with Eight Runs (left) and 10 Runs (right)
Note that the minimum distance between each pair of points in the Latin Hypercube design is smaller than that for the Sphere-Packing design. This is because the Latin Hypercube design constrains the levels of each factor to be evenly spaced. The Sphere-Packing design maximizes the minimum distance without any constraints.