Comparing Sphere-Packing, Latin Hypercube, and Uniform Methods

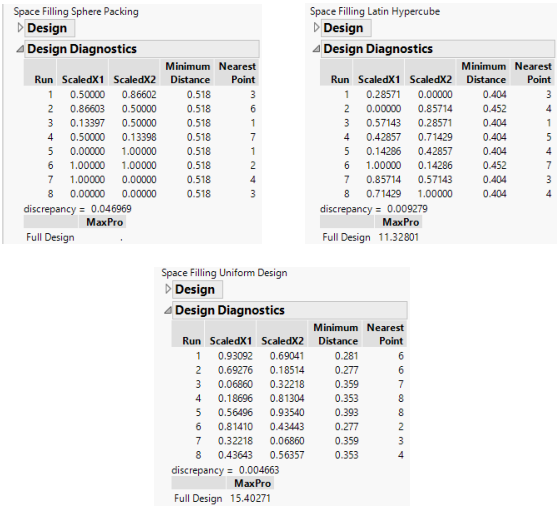
To compare space-filling design methods, create the Sphere Packing, Latin Hypercube, and Uniform designs, as shown in the previous examples. The Design Diagnostics tables show the values for the factors scaled from zero to one. The minimum distance is based on these scaled values and is the minimum distance from each point to its closest neighbor. The discrepancy value is the integrated difference between the design points and the uniform distribution.

Figure 21.16 shows a comparison of the design diagnostics for three eight-run space-filling designs. Note that the discrepancy for the Uniform design is the smallest (best). The discrepancy for the Sphere-Packing design is the largest (worst). The discrepancy for the Latin Hypercube takes an intermediate value that is closer to the optimal value. The MaxPro criteria is smaller for the Latin Hypercube design as compared to the Uniform Design.

Also note that the minimum distance between pairs of points is largest (best) for the Sphere-Packing method. The Uniform design has pairs of points that are only about half as far apart. The Latin Hypercube design behaves more like the Sphere-Packing design in spreading the points out.

For both spread and discrepancy, the Latin Hypercube design represents a healthy compromise solution.

Figure 21.16 Comparison of Diagnostics for Three Eight-Run Space-Filling Methods 

Another point of comparison is the time it takes to compute a design. The Uniform design method requires the most time to compute. Also, the time to compute the design increases rapidly with the number of runs. For comparable problems, all the space-filling design methods take longer to compute than the D-optimal designs in the Custom Designer.